kvl and kcl experiment theory

About Contact Sing up Log in
Business & Industries
Shipping & Logistics
Markets & Trading
Finance & Loan
Automobiles
Cryptocurrency
Beauty & Skin Care
Gift & Jewellery
Pets & Animals
Software & Web Development
Digital Marketing
Latest Technologies
Education & Training
Jobs & Career
Health & Fitness
Medical & Health
Sports & Athletics

To verify the Kirchhoff's voltage law and Kirchhoff's current law for the given circuit

Aim: verification of kirchoff's laws, apparatus required, circuit diagrams, given circuit.

1. KVL Circuit

Practical Circuit for KVL

practical-circuit-diagram-for-kirchoffs-law

2. KCL Circuit

Practical Circuit for KCL

Theory for Kirchhoff's Current and Kirchhoff's Volatage Law

a) Kirchhoff's Voltage law states that the algebraic sum of the voltage around any closed path in a given circuit is always zero. In any circuit, voltage drops across the resistors always have polarities opposite to the source polarity. When the current passes through the resistor, there is a loss in energy and therefore a voltage drop. In any element, the current flows from a higher potential to lower potential. Consider the fig shown above in which there are 3 resistors are in series. According to kickoff's voltage law.

V = V1 + V2 + V3

b) Kirchhoff's current law states that the sum of the currents entering a node equal to the sum of the currents leaving the same node. Consider the fig shown above in which there are 3 parallel paths. According to Kirchhoff's current law.

I = I1 + I2 + I3

Procedure for Kirchhoff's Voltage law:

1. Connect the circuit as shown in fig (2a).

2. Measure the voltages across the resistors.

3. Observe that the algebraic sum of voltages in a closed loop is zero.

Procedure for Kirchhoff's current law:

1. Connect the circuit as shown in fig (2b).

2. Measure the currents through the resistors.

3. Observe that the algebraic sum of the currents at a node is zero.

Observation Table for KVL

Observation table for kcl, precautions.

Avoid loose connections.
Keep all the knobs in minimum position while switch on and off of the supply.

Viva Questions

What is another name for KCL & KVL?
Define network and circuit?
What is the property of inductor and capacitor?

Latest Post

Fashion for Fit Bodies: Expert Styling Tips to Flaunt Your Six Pack Abs

Top 8 Female Casino Streamers Making Waves in 2024

Kirill Yurovskiy: How to Calculate Travel Time

Mastering Pool Cleaning Robot Safety and Efficiency: Your Essential Guide

e-sports-the-perfect-match-for-the-digital-age

E-Sports and Betting: The Perfect Match for the Digital Age

Timur Turlov: Visionary Entrepreneur and Advocate for Financial Innovation

how-to-use-futures-options-for-hedging-strategies

How to Use Futures and Options for Hedging Strategies

Related categories.

Instrumentation & Measurement
Analog & Digital Communication
Analog Electronics
Digital Electronics
Electronic Devices & Circuits
Digital Circuit System
Digital Communication
Electronic Circuit Design
Microprocessor & Interfacing
Electrical Machines 1
Electrical Machines 2
Power Electronics

Electrical Lab Experiment list

1 To conduct Open circuit vs Short circuit tests on single phase transformer
2 To measure the displacement vs to determine the characteristics of LVDT (Linear Variable Differential Transformer).
3 To plot the transistor (BJT) characteristics of CE configuration.
4 To find the forward vs reverse bias characteristics of a given Zener diode.
5 To perform Swinburne's test on the given DC machine
6 To verify the Kirchhoff's voltage law vs Kirchhoff's current law for the given circuit
7 To measure the strain using strain gauge.

Laboratory Experiment Categories

Electrical and Electronics
Civil Engineering
Engineering Mechanics
Mechanical Engineering
Biomedical Engineering

Get all latest content delivered to your email a few times a month.

No category

DC Lab Exp 2(Verification of Kirchhoff s Voltage Law (KVL) and Kirchhoff s Current Law (KCL)-ACS

Add this document to collection(s)

You can add this document to your study collection(s)

Add this document to saved

You can add this document to your saved list

Suggest us how to improve StudyLib

(For complaints, use another form )

Input it if you want to receive answer

AC Circuits
Attenuators
Binary Numbers
Boolean Algebra
Combinational Logic
DC Circuits
Electromagnetism
Input/Output Devices
Logic Gates
Miscellaneous Circuits
Operational Amplifiers
Power Electronics
Power Supplies
RC Networks
Sequential Logic
Transformers
Transistors
Waveform Generators
Premium content
Further Education
Sitemap Page
Connectivity
Input and Output Devices
Premium Content

Kirchhoffs Circuit Law

Kirchhoffs Circuit Laws allow us to solve complex circuit problems by defining a set of basic network laws and theorems for the voltages and currents around a circuit

Using Kirchhoffs circuit law relating to the junction rule and his closed loop rule, we can calculate and find the currents and voltages around any closed circuit providing we know the values of the electrical components within it.

We saw in the Resistors tutorial that a single equivalent resistance, ( R T ) can be found when two or more resistors are connected together in either series, parallel or combinations of both, and that these circuits obey Ohm’s Law.

However, sometimes in complex circuits such as bridge or T networks, we can not simply use Ohm’s Law alone to find the voltages or currents circulating within the circuit. For these types of calculations we need certain rules which allow us to obtain the circuit equations and for this we can use Kirchhoffs Circuit Law .

In 1845, a German physicist, Gustav Kirchhoff developed a pair or set of rules or laws which deal with the conservation of current and energy within electrical circuits. These two rules are commonly known as: Kirchhoffs Circuit Laws with one of Kirchhoffs laws dealing with the current flowing around a closed circuit, Kirchhoffs Current Law, (KCL) while the other law deals with the voltage sources present in a closed circuit, Kirchhoffs Voltage Law, (KVL) .

Kirchhoffs First Law – The Current Law, (KCL)

Kirchhoffs Current Law or KCL, states that the “ total current or charge entering a junction or node is exactly equal to the charge leaving the node as it has no other place to go except to leave, as no charge is lost within the node “. In other words the algebraic sum of ALL the currents entering and leaving a node must be equal to zero, I (exiting) + I (entering) = 0. This idea by Kirchhoff is commonly known as the Conservation of Charge .

Kirchhoffs Current Law

Here, the three currents entering the node, I 1 , I 2 , I 3 are all positive in value and the two currents leaving the node, I 4 and I 5 are negative in value. Then this means we can also rewrite the equation as;

I 1 + I 2 + I 3 – I 4 – I 5 = 0

The term Node in an electrical circuit generally refers to a connection or junction of two or more current carrying paths or elements such as cables and components. Also for current to flow either in or out of a node a closed circuit path must exist. We can use Kirchhoff’s current law when analysing parallel circuits.

Kirchhoffs Second Law – The Voltage Law, (KVL)

Kirchhoffs Voltage Law or KVL, states that “ in any closed loop network being driven by a voltage source, the total voltage around the loop is equal to the sum of all the voltage drops within the same loop ” which is equal to zero. In other words the algebraic sum of all voltage sources and voltage drops within a closed loop must be equal to zero since the algebraic sum of the voltage drops equals the algebraic sum of the voltage sources. This idea by Kirchhoff is known as the Conservation of Energy .

Kirchhoffs Voltage Law

Starting at any point in the loop continue in the same direction noting the direction of all the voltage drops, either positive or negative, and returning back to the same starting point. It is important to maintain the same direction either clockwise or anti-clockwise or the final voltage sum will not be equal to zero. We can use Kirchhoff’s voltage law when analysing series circuits.

When analysing either DC circuits or AC circuits using Kirchhoffs Circuit Laws a number of definitions and terminologies are used to describe the parts of the circuit being analysed such as: node, paths, branches, loops and meshes. These terms are used frequently in circuit analysis so it is important to understand them.

Common DC Circuit Theory Terms:

• Circuit – a circuit is a closed loop conducting path in which an electrical current flows.
• Path – a single line of connecting elements or sources.
• Node – a node is a junction, connection or terminal within a circuit were two or more circuit elements are connected or joined together giving a connection point between two or more branches. A node is indicated by a dot.
• Branch – a branch is a single or group of components such as resistors or a source which are connected between two nodes.
• Loop – a loop is a simple closed path in a circuit in which no circuit element or node is encountered more than once.
• Mesh – a mesh is a single closed loop series path that does not contain any other paths. There are no loops inside a mesh.

Components are said to be connected together in Series if the same current value flows through all the components.

Components are said to be connected together in Parallel if they have the same voltage applied across them.

A Typical DC Circuit

Kirchhoffs circuit law example no1.

Find the current flowing in the 40Ω Resistor, R 3

The circuit has 3 branches, 2 nodes ( A and B ) and 2 independent loops.

Using Kirchhoffs Current Law , KCL the equations are given as:

At node A : I 1 + I 2 = I 3

At node B : I 3 = I 1 + I 2

Using Kirchhoffs Voltage Law , KVL the equations are given as:

Loop 1 is given as : 10 = R 1 I 1 + R 3 I 3 = 10I 1 + 40I 3

Loop 2 is given as : 20 = R 2 I 2 + R 3 I 3 = 20I 2 + 40I 3

Loop 3 is given as : 10 – 20 = 10I 1 – 20I 2

As I 3 is the sum of I 1 + I 2 we can rewrite the equations as;

Eq. No 1 : 10 = 10I 1 + 40(I 1 + I 2 ) = 50I 1 + 40I 2

Eq. No 2 : 20 = 20I 2 + 40(I 1 + I 2 ) = 40I 1 + 60I 2

We now have two “ Simultaneous Equations ” that can be reduced by subtraction to give us the values of I 1 and I 2

Substitution of I 1 in terms of I 2 gives us the value of I 1 as -0.143 Amps

Substitution of I 2 in terms of I 1 gives us the value of I 2 as +0.429 Amps

As : I 3 = I 1 + I 2

The current flowing in resistor R 3 is given as : -0.143 + 0.429 = 0.286 Amps

and the voltage across the resistor R 3 is given as : 0.286 x 40 = 11.44 volts

The negative sign for I 1 means that the direction of current flow initially chosen was wrong, but never the less still valid. In fact, the 20v battery is charging the 10v battery.

Application of Kirchhoffs Circuit Laws

These two laws enable the Currents and Voltages in a circuit to be found, ie, the circuit is said to be “Analysed”, and the basic procedure for using Kirchhoff’s Circuit Laws is as follows:

1. Assume all voltages and resistances are given (If not label them V1, V2,..R1, R2, etc.)
2. Assigns a current to each branch or mesh (clockwise or anticlockwise)
3. Label each branch with a branch current. ( I1, I2, I3 etc. )
4. Find Kirchhoff’s first law equations for each node.
5. Find Kirchhoff’s second law equations for each of the independent loops of the circuit.
6. Use Linear simultaneous equations as required to find the unknown currents.

As well as using Kirchhoffs Circuit Law to calculate the various voltages and currents circulating around a linear circuit, we can also use loop analysis to calculate the currents in each independent loop which helps to reduce the amount of mathematics required by using just Kirchhoff’s laws. In the next tutorial about DC circuits, we will look at Mesh Current Analysis to do just that.

519 Comments

Notify me of follow-up comments by email.

Electronic Tutorial is a very good Website because it calculate & explain Kirchhoff’s Electrical Laws properly. I love this Website because it is fantastic.

I love this site, it really simplified Kirchhoff’s laws.

I want to join.

These things are really helping me so much, but I wonder why registering my name is not working mainly on user name?

Because the user name is already taken

I love this site, very accurate and straight to the point

I need to know more about this topic

This is so helpful

Thanks..you so much its really helpful

Hello, Kirchhoffs Voltage Law example is confusing : it says “the total voltage around the loop is equal to the sum of all the voltage drops within the same loop” ; it does not say : “the sum of all the voltage drops within the same loop equals zero”. So Vab + Vbc + Vcd + Vda would not equal zero (there is no voltage source in this loop in the first place) – Rda should be replaced by a voltage source for the example to be less confusing.

Seems triable good

Pushpendra singh thakur

Continue to you work

Good , can we no more

I like to understand kirchhoff voyage law

You have really helped me understand the Kirchhoff’s thanks

It is really well explained and understandable.

How do we calculate for Kirchhoff’s current

This was really helpful

Privacy Policy
Terms of Use
Contact Sales
Media Guide Request
Electronic Products
Power Electronics News
Planet Analog
ElectroSchematics
Datasheets.com
Electronics Know How
The Channelist
EE Times Asia
EE Times China
EE Times India
EE Times Japan
EE Times Taiwan

To study and verify the Kirchhoff's law.

Introduction:.

“Kirchhoff’s Voltage Law (The Loop Rule) states that around any closed loop or path in a circuit, the algebraic sum of all electric potential differences is equal to zero.”

This law is also called “kirchhoff’s second law”

When the current passes through the resistor, there is a loss in energy and therefore a voltage drop. Kirchhoff’s voltage law.

In any circuit, voltage drops across the resistors have opposite polarities to the source polarity. Remember that when traveling around the circuit to apply Kirchhoff's Voltage Law, be sure you are always going in the same direction (clockwise or counterclockwise) to determine whether a given element represents an increase or decrease in the voltage. If you begin jumping around, moving in different directions, your equation will be When crossing a resistor, the voltage change is determined by the ohm’s law…

where I is the value of the current and R is the resistance of the resistor. Crossing in the same direction as the current means the voltage goes down, so its value is negative. When crossing a resistor in the direction opposite the current, the voltage value is positive, so it is increasing.

In given figure there are two loop. Acc. to Kirchhoff’s voltage law…….

Advantages of Kirchhoff’s Law

Kirchhoff’s Law can easily calculate unknown currents and voltages.

The analysis and simplification of complex closed-loop circuits become manageable.

Disadvantages of Kirchhoff’s Law

Kirchhoff’s rules work on the assumption that the closed loop has no fluctuating magnetic fields. Under the influence of a fluctuating magnetic field, electric fields and electromotive force can be created, causing in Kirchhoff’s rule to be broken.

Kirchhoff’s Current Law or KCL, states that the “total current or charge entering a junction or node is exactly equal to the charge leaving the node as it has no other place to go except to leave, as no charge is lost within the node".

It is also called as Kirchhoff's first law, Kirchhoff's point rule, or Kirchhoff's junction rule (or nodal rule).

This law represents a mathematical statement of the fact that charge cannot accumulate at a node. A node is not a circuit element, and it certainly cannot store, destroy, or generate charge. Hence, the currents must sum to zero. We can use hydraulic analogy here to understand better: for example, let’s consider three water pipes joined in the shape of a Y. We define three water currents as flowing into each of the three pipes. If we insist that water is always flowing, then obviously we cannot have three positive water currents, or the pipes would burst. This is a result of our defining currents independent of the direction that water is actually flowing. Therefore, the value of either one or two of the currents as defined must be negative.

Summarizing,

“The algebraic sum of all currents entering and exiting a node must equal zero” Mathematically,

KCL can be viewed as an extension of the conservation of charge, since charge is the product of current and the time the current has been flowing in the circuit. Kirchhoff’s Current Law is applicable to any lumped parameter electrical circuit.

CIRCUIT DIAGRAM:

Applying KCL at node,

In the above equation, the left-hand side represents the sum of entering currents, whereas the right-hand side represents the sum of leaving currents. Here we will consider positive sign when current leaves a node and negative sign when it enters a node. Similarly, you can consider negative sign when the current leaves a node and positive sign when it enters a node. In both cases, the result will be same. KCL is independent of the nature of network elements that are connected to a node.

Switch skin

Home > Circuit Analysis > Kirchhoff’s Current & Voltage Law (KCL & KVL) | Solved Example

Kirchhoff’s Current & Voltage Law (KCL & KVL) | Solved Example

Kcl & kvl – kirchhoff’s first & second laws with solved example.

A German Physicist “Robert Kirchhoff” introduced two important electrical laws in 1847 by which, we can easily find the equivalent resistance of a complex network and flowing currents in different conductors. Both AC and DC circuits can be solved and simplified by using these simple laws which are known as Kirchhoff’s Current Law (KCL) and Kirchhoff’s Voltage Law (KVL).

Also note that KCL is derived from the charge continuity equation in electromagnetism while KVL is derived from Maxwell – Faraday equation for static magnetic field (the derivative of B with respect to time is 0).

Kirchhoff’s Current Law (KCL):

According to KCL:

At any moment, the algebraic sum of flowing currents through a point (or junction) in a network is Zero (0) or in any electrical network, the algebraic sum of the currents meeting at a point (or junction) is Zero (0). This law is also known as Point Law or Current law.

In any electrical network , the algebraic sum of incoming currents to a point and outgoing currents from that point is Zero. Or the entering currents to a point are equal to the leaving currents of that point.

In other words, the sum of the currents flowing towards a point is equal to the sum of those flowing away from it. Or the algebraic sum of the currents entering a node equals the algebraic sum of the currents leaving it.

Explanation of KCL:

Suppose some conductors are meeting at a point “A” as shown in fig 1.a. In some conductors, currents are incoming to the point “A” while in other conductors, Currents are leaving or outgoing from point “A”.

Consider the incoming or entering currents as “Positive (+) towards point “A” while the leaving or outgoing currents from point “A” is “Negative (-)”. then:

I 1 + ( – I 2 ) + ( – I 3 ) + ( – I 4 ) + I 5 = 0

I 1 + I 5 – I 2 – I 3 – I 4 = 0

I 1 + I 5 = I 2 + I 3 + I 4 = 0

Incoming or Entering Currents = Leaving or Outgoing Currents

Σ I Entering = Σ I Leaving

For instance, 8A is coming towards a point and 5A plus 3A are leaving that point in fig 1.b, therefore,

8A = 5A + 3A

Kirchhoff’s Voltage Law (KVL):

The Kirchhoff’s second law or KVL stated that;

In any closed path (or circuit) in a network, the algebraic sum of the IR product is equal to the EMF in that path.

In other words, in any closed loop (which is also known as Mesh), the algebraic sum of the EMF applied is equal to the algebraic sum of the voltage drops in the elements. Kirchhoff’s second law is also known as Voltage Law or Mesh law.

Explanation of KVL:

A closed circuit is shown in fig which contains two connections of batteries E 1 and E 2 . The overall sum of E.M.F’s of the batteries is indicated by E 1 -E 2 . The imaginary direction of current is also shown in the fig.

E 1 drives the current in such a direction which is supposed to be positive while E 2 interferes in the direction of current (i.e. it is in the opposite direction of the supposed direction of current) hence, it is taken as negative. The voltage drop in this closed circuit depends on the product of Voltage and Current .

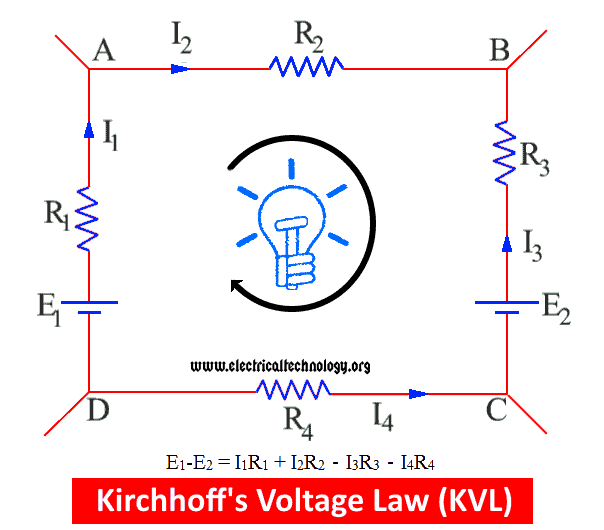
The voltage drop occurs in the supposed direction of current is known as Positive voltage drop while the other one is negative voltage drop.

In the above fig, I 1 R 1 and I 2 R 2 are positive voltage drops and I 3 R 3 and I 4 R 4 are negative V.D.

If we go around the closed circuit (or each mesh), and multiply the resistance of the conductor and the flowing current in it, then the sum of the IR is equal to the sum of the applied EMF sources connected to the circuit.

The overall equation for the above circuit is:

E 1 – E 2 = i 1 R 1 + i 2 R 2 – i 3 R 3 – i 4 R 4

If we go in the supposed direction of the current as shown in the fig, then the product of the IR is taken as positive otherwise negative.

Good to Know:

Direction of the Current:

It is very important to determine the direction of current whenever solving circuits via Kirchhoff’s laws. Same like the case of election current and conventional current .

The direction of current can be assumed through clockwise or anticlockwise direction. Once you select the custom direction of the current, you will have to apply and maintain the same direction for the overall circuit until the final solution of the circuit.

If we got the final value as positive it means, the supposed direction of the current was correct. In case of negative values, the current of the direction is reversed as compared to the supposed one then.

Circuit Analysis by Kirchhoff’s Laws

Solved Example on KCL and KVL (Kirchhoff’s Laws)

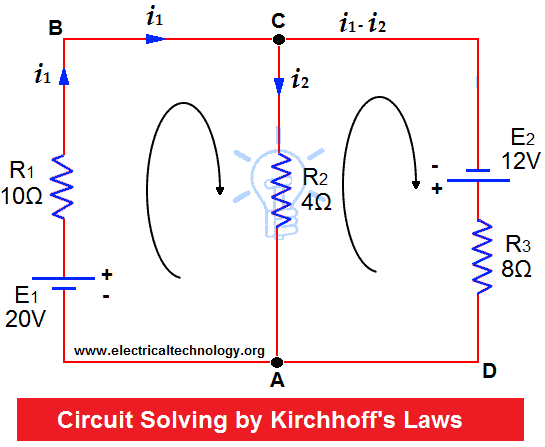
Assume currents to flow in directions indicated by arrows.

Apply KCL on Junctions C and A.

Therefore, current in mesh ABC = i 1

Current in Mesh CA = i 2

Then current in Mesh CDA = i 1 – i 2

Now, Apply KVL on Mesh ABC, 20V are acting in clockwise direction. Equating the sum of IR products, we get;

10 i 1 + 4 i 2 = 20 … (1)

In mesh ACD, 12 volts are acting in clockwise direction, then:

8( i 1 – i 2 ) – 4 i 2 = 12

8 i 1 – 8 i 2 – 4 i 2 = 12

8 i 1 – 12 i 2 = 12 … (2)

Multiplying equation (1) by 3;

30 i 1 + 12 i 2 = 60

Solving for i 1

8 i 1 – 12 i 2 = 12

___________ 38 i 1 = 72

The above equation can be also simplified by Elimination or Cramer’s Rule .

i 1 = 72 ÷ 38 = 1.895 Amperes = Current in 10 Ohms resistor

Substituting this value in (1), we get:

10 (1.895) + 4 i 2 = 20

4 i 2 = 20 – 18.95

i 2 = 0.263 Amperes = Current in 4 Ohms Resistors.

i 1 – i 2 = 1.895 – 0.263 = 1.632 Amperes

Applications of Kirchhoff’s Laws

Kirchhoff’s laws can be used to determine the values of unknown values like current and Voltage as well as the direction of the flowing values of these quintets in the circuit.
These laws can be applied on any circuit* (See the limitation of Kirchhoff’s Laws at the end of the article), but useful to find the unknown values in complex circuits and networks.
Also used in Nodal and Mesh analysis to find the values of current and voltage.
Current through each independent loop is carried by applying KVL (each loop) and current in any element of a circuit by counting all the current (Applicable in Loop Current Method).
Current through each branch is carried by applying KCL (each junction) KVL in each loop of a circuit (Applicable in Loop Current Method).
Kirchhoff’s Laws are useful in understanding the transfer of energy through an electric circuit.

Good To Know:

These rules of thumbs must be taken into account while simplifying and analyzing electric circuits by Kirchhoff’s Laws:

The Voltage Drop in a loop due to current in clockwise direction is considered as Positive (+) Voltage Drop.
The Voltage Drop in a loop due to current in anticlockwise direction is considered as Negative (-) Voltage Drop.
The deriving current by the battery in clockwise direction is taken as Positive (+).
The deriving current by the battery in anticlockwise direction is taken as Positive (-).

Limitations of Kirchhoff’s laws:

KCL is applicable on the assumption that current flows only in conductors and wires. While in High Frequency circuits where, parasitic capacitance can no longer be ignored. In such cases, Current can flow in an open circuit because in these cases, conductors or wires are acting as transmission lines.
KVL is applicable on the assumption that there is no fluctuating magnetic field linking the closed loop. While, in presence of changing magnetic field in a High Frequency but short wave length AC circuits, the electric field is not a conservative vector field. So, the electric field cannot be the gradient of any potential and the line integral of the electric field around the loop is not zero, directly contradicting KVL. That’s why KVL is not applicable in such a condition.
During the transfer of energy from the magnetic field to the electric field where fudge has to be introduced to KVL to make the P.d ( potential differences ) around the circuit equal to 0.

Related Posts about electric circuits analysis theorems:

Thevenin’s Theorem. Step by Step Procedure with Solved Example
Norton’s Theorem. Easy Step by Step Procedure with Example (Pictorial Views)
SUPERNODE Circuit Analysis | Step by Step with Solved Example
SUPERMESH Circuit Analysis | Step by Step with Solved Example
Maximum Power Transfer Theorem for AC & DC Circuits
Compensation Theorem – Proof, Explanation and Solved Examples
Substitution Theorem – Step by Step Guide with Solved Example
Millman’s Theorem – Analyzing AC & DC Circuits – Examples
Superposition Theorem – Circuit Analysis with Solved Example
Tellegen’s Theorem – Solved Examples & MATLAB Simulation
Voltage Divider Rule (VDR) – Solved Examples for R, L and C Circuits
Current Divider Rule (CDR) – Solved Examples for AC and DC Circuits
Ohm’s Law: Simple Explanation with Statement and Formulas
Star to Delta & Delta to Star Conversion. Y-Δ Transformation

Electrical Technology

How to Size a Single Phase and Three Phase Transformer in kVA? Calculator

Battery Charging Current and Battery Charging Time formula with 120Ah battery solved examples

How to Calculate the Battery Charging Time & Battery Charging Current – Example

How To Calculate Your Electricity Bill Simple Calculation.

How To Calculate Your Electricity Bill. Electric Bill Calculator with Examples

How to Find The Correct Size of Cable & Wire in NEC, IET and IEC

How to Find the Proper Size of Wire & Cable In Metric & Imperial Systems

Thevenin's Theorem. Easy Step by Step Procedure with Example (Pictorial Views)

Thevenin’s Theorem. Step by Step Procedure with Solved Example

Dark Detector Circuit for Automatic Street Light Control using BC547 Transistor and LDR

Automatic Street Light Control Circuit using LDR & Transistor BC 547

24 comments.

electrical advance system fault analysis

There’s a mistake in the solved example.. I’m the second loop, the equation should be 8(i1–i2)- 4i2= 12

The -4i2 is missing

Thanks for correction.

according to Kirchhoff’s voltage law the voltage drops is equal to the resultant e.m.f acting on that loop. So following the current in the second loop, there was a voltage lift at the at the second supply voltage thus having it as positive 12 (+12). Then the current went from this to the 8ohm resistor which causes a voltage drop thus making it -8(i1-i2). Then loop continued to the 4ohm resister which had a voltage drop from positive to negative thus having -4i2 so for me the equation should look like this 12-8(i1-i2)-4i2=0 so that 12 -8i1+8i2-4i2=0 which is 12-8i1+4i2=0 so the final equation for loop two will be 12=8i1-4i2 if I’ve done any mistake please correct me

in kvl method why we are going to multiply the equation 1 by 3?

Now, Apply KVL on Mesh ABC, 20V are acting in clockwise direction. Equating the sum of IR products, we get; 10i1 + 4i2 = 20 ……………. (1)

In mesh ACD, 12 volts are acting in clockwise direction, then: 8(i1–i2) – 4i2= 12 8i1 – 8i2 – 4i2= 12 8i1 – 12i2 = 12 ……………. (2) Multiplying equation (1) by 3; 30i1 + 12i2 = 60

It is a simple elimination… You can Also do it by Cramer’s Rule …

bcz we have to just cancel out i2 so we can find out i1 value

How do you now with what do you need to eliminate the equation?Why 3 and not 2 for example?

please, I need the final answer of this equation

Whay you multiple by 3 .i can’t get it plizzz tell me …whay only 3 whay not 2&3&4&5&3 some like

how can i determine the current direction if i am not given

simple you can make your own assumption by drawing direction of current from any junction you want

If your answer will be nagative you have to oppose the direction you assumed

good, excellent & lucid way to explain them.

I enjoyed the explanation of Kcl and kvl. Can you solve questions of a circuit which has more two sources of voltage.

little bit confused

Simply nice

I’m not sure about current law

good example .please uplode more question about this topic ,mean kvl or kcl

i didn’t touch ur idea about kvl. I think we just needed here to apply kvl in each mesh i1(10) + (i1 – i2)(4)= 20 i2(8) + (i2 – i1)(4)= 12 now needed to solve these two equations by crammer’s rule or by simplification…

Thank your for the details and infor about KVL and KCL.

I would like to object to this statement in your article: The voltage drop in this closed circuit depends on the product of Voltage and Current.

Verification of Kirchhoff’s Voltage and Current laws

Experiment Number: 01

Aim of the Experiment: –

Verification of Kirchhoff’s Voltage Law (KVL) and Kirchhoff’s Current Law (KCL).

Apparatus Required: –

CIRCUIT DIAGRAM: –

Theory: –

Kirchhoff’s Voltage Law- It states that the algebraic sum of voltage drops in elements & voltage sources in any closed path (or mesh) in an electric network is equal to zero.

Let us assuming the above fig. By applying KVL in closed path (or loop ) V-IR 1 -IR 2 =0 or V=IR 1 +IR 2

Kirchhoff’s Current Law – It states that in any electrical circuit or network, the algebraic sum of currents meeting at any node (or junction or point) is equal to zero.

Let us assume an electrical network as shown above. ‘A’ is the junction (or node) where all currents are meeting. Assuming incoming current is +ve & outgoing currents are –ve at point ‘A’. Then I-I 1 -I 2 =0 or I=I 1 +I 2 or ΣI=0

Procedures: –

All Instruments are connected as per circuit diagram shown in fig.
The voltage is increased gradually by single phase auto- transformer & corresponding readings of Voltmeters & Ammeters are filled in observation table.

Precautions: –

Don’t switch on power supply without concerning teacher.
Single phase autotransformer must be kept at minimum potential point before switch on the experiment.

Observation Table: –

For KVL: –

For KCL: –

Conclusion:-

To be written by student.

For Your Reference: –

Kirchhoff’s Voltage Law (KVL) and Kirchhoff’s Current Law (KCL) are fundamental principles in electrical engineering and circuit analysis.

Kirchhoff’s Voltage Law (KVL) : It states that the algebraic sum of the voltage drops (i.e., voltage across elements) in any closed loop of a circuit is equal to zero. This law is based on the principle of conservation of energy, stating that the total energy supplied to a closed loop must be equal to the total energy consumed. Mathematically, for a closed loop:

Where 𝑉𝑛 is the voltage across the n th element in the loop and 𝑁 is the total number of elements in the loop.

2. Kirchhoff’s Current Law (KCL) : It states that the algebraic sum of currents entering a node (or a closed boundary) in an electrical circuit is zero. This law is based on the principle of conservation of charge, stating that the total charge entering a node must equal the total charge leaving it.

Mathematically, for a node:

Verification of these laws involves applying them to different circuits and analyzing whether they hold true. It’s important to ensure that the assumptions and conventions used in circuit analysis, such as sign conventions for voltage and current, are consistent with the application of these laws.

Some Viva-voce questions:

KVL states that the sum of voltages around any closed loop in a circuit is zero. It’s important because it’s based on the conservation of energy principle and provides a systematic method for analyzing complex circuits.
In circuit analysis, KVL is applied by traversing a closed loop in a circuit and summing up the voltage drops across all elements ( resistors, capacitors, and inductors ) encountered in the loop. The algebraic sum of these voltage drops must equal zero.
The assumptions include the ideal behavior of circuit elements (like resistors having linear voltage-current characteristics), no significant electromagnetic interference, and steady-state conditions unless stated otherwise.
KCL states that the algebraic sum of currents at any node (or junction) in a circuit is zero, based on the conservation of charge principle. It’s crucial for analyzing current distribution in complex circuits and ensures that the current entering a node equals the current leaving it.
In circuit analysis, KCL is applied by summing up currents at each node, ensuring that the sum equals zero. This involves assigning currents entering the node as positive and currents leaving as negative, following a sign convention.
If these laws appear to be violated, it usually indicates errors in circuit analysis, such as incorrect application of the laws, incorrect assumptions about circuit behavior, or faulty measurements. Revisiting the analysis and ensuring all conditions are met typically resolves such discrepancies.
An example could be analyzing a circuit with multiple loops and nodes, such as a series-parallel circuit with resistors. Applying KVL to each loop and KCL to each node would help determine the currents and voltages across different elements in the circuit. (Explain with Circuit Diagram)