- Solve equations and inequalities
- Simplify expressions
- Factor polynomials
- Graph equations and inequalities
- Advanced solvers
- All solvers
- Arithmetics
- Determinant
- Percentages
- Scientific Notation
- Inequalities

What can QuickMath do?
QuickMath will automatically answer the most common problems in algebra, equations and calculus faced by high-school and college students.
- The algebra section allows you to expand, factor or simplify virtually any expression you choose. It also has commands for splitting fractions into partial fractions, combining several fractions into one and cancelling common factors within a fraction.
- The equations section lets you solve an equation or system of equations. You can usually find the exact answer or, if necessary, a numerical answer to almost any accuracy you require.
- The inequalities section lets you solve an inequality or a system of inequalities for a single variable. You can also plot inequalities in two variables.
- The calculus section will carry out differentiation as well as definite and indefinite integration.
- The matrices section contains commands for the arithmetic manipulation of matrices.
- The graphs section contains commands for plotting equations and inequalities.
- The numbers section has a percentages command for explaining the most common types of percentage problems and a section for dealing with scientific notation.
Math Topics
More solvers.
- Add Fractions
- Simplify Fractions

Kristy Lee L.
8.9 Variation and Problem Solving
The force F needed to break a board varies inversely with the length l of the board. If it takes 24 pounds of pressure to break a board 2 feet long, how many pounds of pressure will it take to break a board that is 5 feet long? Give your answer as a decimal and do not include units.
1 Expert Answer

Patrick B. answered • 08/21/19
Math and computer tutor/teacher
FOr L=5, F = 96/5^2 = 96/25 = 3.84 pounds per square foot
Still looking for help? Get the right answer, fast.
Get a free answer to a quick problem. Most questions answered within 4 hours.
Choose an expert and meet online. No packages or subscriptions, pay only for the time you need.
RELATED TOPICS
Related questions, 4.5 yds = ____ ft.
Answers · 7
8 hits in 22 games
Answers · 2
What is the best way to teach a 4th grader with ADD multiplication tables? He struggles with his lack of attention so memorization isn't working.
Answers · 22
How do you add 6/5 + 1/4? Thank you
Answers · 15
How can one division expression have more than one answer?
Recommended tutors.

find an online tutor
- Math tutors
- Discrete Math tutors
- Advanced College Math tutors
- 7th Grade Math tutors
- ACCUPLACER College-Level Math tutors
- ACT Math tutors
- College Math tutors
- SAT Math tutors
related lessons
- Elementary Math Help
- SAT Math Test Format and Strategies
- ACT Math Test Format and Strategies
- Prealgebra Math Help
- Math Resources and Math Lessons
- GRE Quant Test Format and Strategies
- How to Estimate
- AP Calculus
- AP Statistics
- Independent Study
Online Math Class
Mr. Math Blog
Thanks for your donation! Every little bit helps me help you! :-)
Problem Solving - Organize Data - Lesson 2.1
Use Picture Graphs - Lesson 2.2
Make Picture Graphs - Lesson 2.3
Use Bar Graphs - Lesson 2.4
Make a Bar Graph - Lesson 2.5
Solve Problems Using Data - Lesson 2.6
Use and Make Line Plots - Lesson 2.7
Number Patterns - Lesson 1.1
Round to Nearest Ten or Hundred - Lesson 1.2
Estimate Sums - Lesson 1.3
Mental Math Strategies for Addition - Lesson 1.4
Use Properties to Add - Lesson 1.5
Use the Break Apart Strategy to Add - Lesson 1.6
Use Place Value to Add - Lesson 1.7
Estimate Differences - Lesson 1.8
Mental Math Strategies for Subtraction - Lesson 1.9
Use Place Value to Subtract - Lesson 1.10
Combine Place Values to Subtract - Lesson 1.11
Describe Plane Shapes - Lesson 12.1
Describe Angles in Plane Shapes - Lesson 12.2
Identify Polygons - Lesson 12.3
Describe Sides of Polygons - Lesson 12.4
Classify Quadrilaterals - Lesson 12.5
Draw Quadrilaterals - Lesson 12.6
Describe Triangles - Lesson 12.7
Chapter 12 Performance Task Review For Test
Problem Solving - Compare Fractions - Lesson 9.1
Compare Fractions with the Same Denominator - Lesson 9.2
Compare Fractions with the Same Numerator - Lesson 9.3
Compare Fractions - Lesson 9.4
Compare and Order Fractions - Lesson 9.5
Model Equivalent Fractions - Lesson 9.6
Equivalent Fractions - Lesson 9.7
Divide by 2 - Lesson 7.1
Divide by 10 - Lesson 7.2
Divide by 5 - Lesson 7.3
Divide by 3 - Lesson 7.4
Divide by 4 - Lesson 7.5
Divide by 5 - Lesson 7.6
Mid-Chapter 7 Checkpoint on Division Facts and Strategies
Divide by 7 - Lesson 7.7
Divide by 8 - Lesson 7.8
Divide by 9 - Lesson 7.9
Problem Solving - Two-Step Problems - Lesson 7.10
Order of Operations - Lesson 7.11
Problem Solving - Model Division - Lesson 6.1
Size of Equal Groups - Lesson 6.2
Number of Equal Groups - Lesson 6.3
Model (Division) with Bar Model - Lesson 6.4
Relate Subtraction and Division - Lesson 6.5
Mid-Chapter 6 Checkpoint
Model (division) with Arrays - Lesson 6.6
Relate Multiplication and Division - Lesson 6.7
Write Related Facts - Lesson 6.8
Division Rules for 1 and 0 - Lesson 6.9
Chapter 6 Review for Test - Understanding Division
Multiply with 2 and 4 - Lesson 4.1
Multiply with 5 and 10 - Lesson 4.2
Multiply with 3 and 6 - Lesson 4.3
Distributive Property - Lesson 4.4
Multiply with 7 - Lesson 4.5
Associative Property of Multiplication - Lesson 4.6
Patterns on the Multiplication Table - Lesson 4.7
Multiply with 8 - Lesson 4.8
Multiply with 9 - Lesson 4.9
Review For Test on Chapter 4
Describe Patterns - Lesson 5.1
Find Unknown Factors - Lesson 5.2
Problem Solving: Using the Distributive Property - Lesson 5.3
Multiplication Strategies with Multiples of 10 - Lesson 5.4
Multiply Multiples of 10 by 1-Digit Numbers - Lesson 5.5
Chapter 5 Review on Multiplication Facts
Third Grade
Math
- Second Grade Math
- Third Grade Math
- Fourth Grade Math
- Fifth Grade Math
- Sixth Grade Math
- Sixth Grade Math (CA)
- Seventh Grade Math (CA)
- Eighth Grade Math (CA)
- Integrated Math 1
- Integrated Math 2
- Integrated Math 3
- PreCalculus
- AP Statistics Exam Prep
- Elementary Statistics
- ELM Practice
- Percents and Decimals
- Sixth Grade Math (Big Ideas)
Model Perimeter - Lesson 11.1
Find Perimeter - Lesson 11.2
Find Unknown Side Lengths - Lesson 11.3
Understanding Area - Lesson 11.4
Measure Area - Lesson 11.5
Use Area Models - Lesson 11.6
Problem Solving - Area of Rectangles - Lesson 11.7
Area of Combined Rectangles - Lesson 11.8
Same Perimeter - Different Area - Lesson 11.9
Same Area - Different Perimeter - Lesson 11.10
Chapter 11 Review for Test on Perimeter and Area
Please Donate, if you're a regular!
The donate link is below. Thanks so much!!
Count Equal Groups - Lesson 3.1
Relate Addition and Multiplication - Lesson 3.2
Skip Count on a Number Line - Lesson 3.3
Problem Solving - Model Multiplication - Lesson 3.4
Model with Arrays - Lesson 3.5
Commutative Property of Multiplication - Lesson 3.6
Multiply with 1 and 0 - Lesson 3.7
Time to the Minute - Lesson 10.1
A.M. and P.M. - Lesson 10.2
Measure Time Intervals - Lesson 10.3
Use Time Intervals - Lesson 10.4
Problem Solving - Time Intervals - Lesson 10.5
Measure Length - Lesson 10.6
Estimate and Measure Liquid Volume - Lesson 10.7
Estimate and Measure Mass - Lesson 10.8
Equal Parts of a Whole - Lesson 8.1
Equal Shares - Lesson 8.2
Unit Fractions of a Whole - Lesson 8.3
Fractions of a Whole - Lesson 8.4
Fractions on a Number Line - Lesson 8.5
Relate Fractions and Whole Numbers - Lesson 8.6
Fractions of a Group - Lesson 8.7
Find Part of Group Using Unit Fractions - Lesson 8.8
Problem Solving: Find the Whole Using Unit Fractions - Lesson 8.9
Copyright 2013. All rights reserved.
5.1 Solve Systems of Equations by Graphing
Learning objectives.
By the end of this section, you will be able to:
- Determine whether an ordered pair is a solution of a system of equations
- Solve a system of linear equations by graphing
- Determine the number of solutions of linear system
- Solve applications of systems of equations by graphing
Be Prepared 5.1
Before you get started, take this readiness quiz.
For the equation y = 2 3 x − 4 y = 2 3 x − 4 ⓐ is ( 6 , 0 ) ( 6 , 0 ) a solution? ⓑ is ( −3 , −2 ) ( −3 , −2 ) a solution? If you missed this problem, review Example 2.1 .
Be Prepared 5.2
Find the slope and y -intercept of the line 3 x − y = 12 3 x − y = 12 . If you missed this problem, review Example 4.42 .
Be Prepared 5.3
Find the x - and y -intercepts of the line 2 x − 3 y = 12 2 x − 3 y = 12 . If you missed this problem, review Example 4.21 .
Determine Whether an Ordered Pair is a Solution of a System of Equations
In Solving Linear Equations and Inequalities we learned how to solve linear equations with one variable. Remember that the solution of an equation is a value of the variable that makes a true statement when substituted into the equation.
Now we will work with systems of linear equations , two or more linear equations grouped together.
System of Linear Equations
When two or more linear equations are grouped together, they form a system of linear equations.
We will focus our work here on systems of two linear equations in two unknowns. Later, you may solve larger systems of equations.
An example of a system of two linear equations is shown below. We use a brace to show the two equations are grouped together to form a system of equations.
A linear equation in two variables, like 2 x + y = 7, has an infinite number of solutions. Its graph is a line. Remember, every point on the line is a solution to the equation and every solution to the equation is a point on the line.
To solve a system of two linear equations, we want to find the values of the variables that are solutions to both equations. In other words, we are looking for the ordered pairs ( x , y ) that make both equations true. These are called the solutions to a system of equations .
Solutions of a System of Equations
Solutions of a system of equations are the values of the variables that make all the equations true. A solution of a system of two linear equations is represented by an ordered pair ( x , y ).
To determine if an ordered pair is a solution to a system of two equations, we substitute the values of the variables into each equation. If the ordered pair makes both equations true, it is a solution to the system.
Let’s consider the system below:
Is the ordered pair ( 2 , −1 ) ( 2 , −1 ) a solution?
The ordered pair (2, −1) made both equations true. Therefore (2, −1) is a solution to this system.
Let’s try another ordered pair. Is the ordered pair (3, 2) a solution?
The ordered pair (3, 2) made one equation true, but it made the other equation false. Since it is not a solution to both equations, it is not a solution to this system.
Example 5.1
Determine whether the ordered pair is a solution to the system: { x − y = −1 2 x − y = −5 { x − y = −1 2 x − y = −5
ⓐ ( −2 , −1 ) ( −2 , −1 ) ⓑ ( −4 , −3 ) ( −4 , −3 )
Determine whether the ordered pair is a solution to the system: { 3 x + y = 0 x + 2 y = −5 . { 3 x + y = 0 x + 2 y = −5 .
ⓐ ( 1 , −3 ) ( 1 , −3 ) ⓑ ( 0 , 0 ) ( 0 , 0 )
Determine whether the ordered pair is a solution to the system: { x − 3 y = −8 −3 x − y = 4 . { x − 3 y = −8 −3 x − y = 4 .
ⓐ ( 2 , −2 ) ( 2 , −2 ) ⓑ ( −2 , 2 ) ( −2 , 2 )
Solve a System of Linear Equations by Graphing
In this chapter we will use three methods to solve a system of linear equations. The first method we’ll use is graphing.
The graph of a linear equation is a line. Each point on the line is a solution to the equation. For a system of two equations, we will graph two lines. Then we can see all the points that are solutions to each equation. And, by finding what the lines have in common, we’ll find the solution to the system.
Most linear equations in one variable have one solution, but we saw that some equations, called contradictions, have no solutions and for other equations, called identities, all numbers are solutions.
Similarly, when we solve a system of two linear equations represented by a graph of two lines in the same plane, there are three possible cases, as shown in Figure 5.2 :
For the first example of solving a system of linear equations in this section and in the next two sections, we will solve the same system of two linear equations. But we’ll use a different method in each section. After seeing the third method, you’ll decide which method was the most convenient way to solve this system.
Example 5.2
How to solve a system of linear equations by graphing.
Solve the system by graphing: { 2 x + y = 7 x − 2 y = 6 . { 2 x + y = 7 x − 2 y = 6 .
Solve the system by graphing: { x − 3 y = −3 x + y = 5 . { x − 3 y = −3 x + y = 5 .
Solve the system by graphing: { − x + y = 1 3 x + 2 y = 12 . { − x + y = 1 3 x + 2 y = 12 .
The steps to use to solve a system of linear equations by graphing are shown below.
To solve a system of linear equations by graphing.
- Step 1. Graph the first equation.
- Step 2. Graph the second equation on the same rectangular coordinate system.
- Step 3. Determine whether the lines intersect, are parallel, or are the same line.
- If the lines intersect, identify the point of intersection. Check to make sure it is a solution to both equations. This is the solution to the system.
- If the lines are parallel, the system has no solution.
- If the lines are the same, the system has an infinite number of solutions.
Example 5.3
Solve the system by graphing: { y = 2 x + 1 y = 4 x − 1 . { y = 2 x + 1 y = 4 x − 1 .
Both of the equations in this system are in slope-intercept form, so we will use their slopes and y -intercepts to graph them. { y = 2 x + 1 y = 4 x − 1 { y = 2 x + 1 y = 4 x − 1
| Find the slope and -intercept of the first equation. | |
| Find the slope and -intercept of the first equation. | |
| Graph the two lines. | |
| Determine the point of intersection. | The lines intersect at (1, 3). |
| Check the solution in both equations. | |
| The solution is (1, 3). |
Solve each system by graphing: { y = 2 x + 2 y = − x − 4 . { y = 2 x + 2 y = − x − 4 .
Solve each system by graphing: { y = 3 x + 3 y = − x + 7 . { y = 3 x + 3 y = − x + 7 .
Both equations in Example 5.3 were given in slope–intercept form. This made it easy for us to quickly graph the lines. In the next example, we’ll first re-write the equations into slope–intercept form.
Example 5.4
Solve the system by graphing: { 3 x + y = −1 2 x + y = 0 . { 3 x + y = −1 2 x + y = 0 .
We’ll solve both of these equations for y y so that we can easily graph them using their slopes and y -intercepts. { 3 x + y = −1 2 x + y = 0 { 3 x + y = −1 2 x + y = 0
| Solve the first equation for . Find the slope and -intercept. Solve the second equation for . Find the slope and -intercept. | |
| Graph the lines. | |
| Determine the point of intersection. | The lines intersect at (−1, 2). |
| Check the solution in both equations. | |
| The solution is (−1, 2). |
Solve each system by graphing: { − x + y = 1 2 x + y = 10 . { − x + y = 1 2 x + y = 10 .
Solve each system by graphing: { 2 x + y = 6 x + y = 1 . { 2 x + y = 6 x + y = 1 .
Usually when equations are given in standard form, the most convenient way to graph them is by using the intercepts. We’ll do this in Example 5.5 .
Example 5.5
Solve the system by graphing: { x + y = 2 x − y = 4 . { x + y = 2 x − y = 4 .
We will find the x - and y -intercepts of both equations and use them to graph the lines.
| To find the intercepts, let = 0 and solve for , then let = 0 and solve for . | ||
| To find the intercepts, let = 0 then let = 0. | ||
| Graph the line. | ||
| Determine the point of intersection. | The lines intersect at (3, −1). | |
| Check the solution in both equations. | The solution is (3, −1). |
Solve each system by graphing: { x + y = 6 x − y = 2 . { x + y = 6 x − y = 2 .
Try It 5.10
Solve each system by graphing: { x + y = 2 x − y = −8 . { x + y = 2 x − y = −8 .
Do you remember how to graph a linear equation with just one variable? It will be either a vertical or a horizontal line.
Example 5.6
Solve the system by graphing: { y = 6 2 x + 3 y = 12 . { y = 6 2 x + 3 y = 12 .
| We know the first equation represents a horizontal line whose -intercept is 6. | |
| The second equation is most conveniently graphed using intercepts. | |
| To find the intercepts, let = 0 and then = 0. | |
| Graph the lines. | |
| Determine the point of intersection. | The lines intersect at (−3, 6). |
| Check the solution to both equations. | |
| The solution is (−3, 6). |
Try It 5.11
Solve each system by graphing: { y = −1 x + 3 y = 6 . { y = −1 x + 3 y = 6 .
Try It 5.12
Solve each system by graphing: { x = 4 3 x − 2 y = 24 . { x = 4 3 x − 2 y = 24 .
In all the systems of linear equations so far, the lines intersected and the solution was one point. In the next two examples, we’ll look at a system of equations that has no solution and at a system of equations that has an infinite number of solutions.
Example 5.7
Solve the system by graphing: { y = 1 2 x − 3 x − 2 y = 4 . { y = 1 2 x − 3 x − 2 y = 4 .
| To graph the first equation, we will use its slope and -intercept. | |
| To graph the second equation, we will use the intercepts. | |
| Graph the lines. | |
| Determine the point of intersection. | The lines are parallel. |
| Since no point is on both lines, there is no ordered pair that makes both equations true. There is no solution to this system. |
Try It 5.13
Solve each system by graphing: { y = − 1 4 x + 2 x + 4 y = − 8 . { y = − 1 4 x + 2 x + 4 y = − 8 .
Try It 5.14
Solve each system by graphing: { y = 3 x − 1 6 x − 2 y = 6 . { y = 3 x − 1 6 x − 2 y = 6 .
Example 5.8
Solve the system by graphing: { y = 2 x − 3 −6 x + 3 y = − 9 . { y = 2 x − 3 −6 x + 3 y = − 9 .
| Find the slope and -intercept of the first equation. | |
| Find the intercepts of the second equation. | |
| Graph the lines. | |
| Determine the point of intersection. | The lines are the same! |
| Since every point on the line makes both equations true, there are infinitely many ordered pairs that make both equations true. | |
| There are infinitely many solutions to this system. |
Try It 5.15
Solve each system by graphing: { y = − 3 x − 6 6 x + 2 y = − 12 . { y = − 3 x − 6 6 x + 2 y = − 12 .

Try It 5.16
Solve each system by graphing: { y = 1 2 x − 4 2 x − 4 y = 16 . { y = 1 2 x − 4 2 x − 4 y = 16 .
If you write the second equation in Example 5.8 in slope-intercept form, you may recognize that the equations have the same slope and same y -intercept.
When we graphed the second line in the last example, we drew it right over the first line. We say the two lines are coincident. Coincident lines have the same slope and same y -intercept.
Coincident Lines
Coincident lines have the same slope and same y -intercept.
Determine the Number of Solutions of a Linear System
There will be times when we will want to know how many solutions there will be to a system of linear equations, but we might not actually have to find the solution. It will be helpful to determine this without graphing.
We have seen that two lines in the same plane must either intersect or are parallel. The systems of equations in Example 5.2 through Example 5.6 all had two intersecting lines. Each system had one solution.
A system with parallel lines, like Example 5.7 , has no solution. What happened in Example 5.8 ? The equations have coincident lines , and so the system had infinitely many solutions.
We’ll organize these results in Figure 5.3 below:
Parallel lines have the same slope but different y -intercepts. So, if we write both equations in a system of linear equations in slope–intercept form, we can see how many solutions there will be without graphing! Look at the system we solved in Example 5.7 .
The two lines have the same slope but different y -intercepts. They are parallel lines.
Figure 5.4 shows how to determine the number of solutions of a linear system by looking at the slopes and intercepts.
Let’s take one more look at our equations in Example 5.7 that gave us parallel lines.
When both lines were in slope-intercept form we had:
Do you recognize that it is impossible to have a single ordered pair ( x , y ) ( x , y ) that is a solution to both of those equations?
We call a system of equations like this an inconsistent system . It has no solution.
A system of equations that has at least one solution is called a consistent system .
Consistent and Inconsistent Systems
A consistent system of equations is a system of equations with at least one solution.
An inconsistent system of equations is a system of equations with no solution.
We also categorize the equations in a system of equations by calling the equations independent or dependent . If two equations are independent equations , they each have their own set of solutions. Intersecting lines and parallel lines are independent.
If two equations are dependent, all the solutions of one equation are also solutions of the other equation. When we graph two dependent equations , we get coincident lines.
Independent and Dependent Equations
Two equations are independent if they have different solutions.
Two equations are dependent if all the solutions of one equation are also solutions of the other equation.
Let’s sum this up by looking at the graphs of the three types of systems. See Figure 5.5 and Figure 5.6 .
Example 5.9
Without graphing, determine the number of solutions and then classify the system of equations: { y = 3 x − 1 6 x − 2 y = 12 . { y = 3 x − 1 6 x − 2 y = 12 .
| We will compare the slopes and intercepts of the two lines. | |
| The first equation is already in slope-intercept form. | |
| Write the second equation in slope-intercept form. | |
| Find the slope and intercept of each line. | |
| Since the slopes are the same and -intercepts are different, the lines are parallel. |
A system of equations whose graphs are parallel lines has no solution and is inconsistent and independent.
Try It 5.17
Without graphing, determine the number of solutions and then classify the system of equations.
{ y = − 2 x − 4 4 x + 2 y = 9 { y = − 2 x − 4 4 x + 2 y = 9
Try It 5.18
{ y = 1 3 x − 5 x − 3 y = 6 { y = 1 3 x − 5 x − 3 y = 6
Example 5.10
Without graphing, determine the number of solutions and then classify the system of equations: { 2 x + y = − 3 x − 5 y = 5 . { 2 x + y = − 3 x − 5 y = 5 .
| We will compare the slope and intercepts of the two lines. | ||
| Write both equations in slope-intercept form. | ||
| Find the slope and intercept of each line. | ||
| Since the slopes are different, the lines intersect. | ||
A system of equations whose graphs are intersect has 1 solution and is consistent and independent.
Try It 5.19
{ 3 x + 2 y = 2 2 x + y = 1 { 3 x + 2 y = 2 2 x + y = 1
Try It 5.20
{ x + 4 y = 12 − x + y = 3 { x + 4 y = 12 − x + y = 3
Example 5.11
Without graphing, determine the number of solutions and then classify the system of equations. { 3 x − 2 y = 4 y = 3 2 x − 2 { 3 x − 2 y = 4 y = 3 2 x − 2
| We will compare the slopes and intercepts of the two lines. | |
| Write the first equation in slope-intercept form. | |
| The second equation is already in slope-intercept form. | |
| Since the slopes are the same, they have the same slope and same -intercept and so the lines are coincident. |
A system of equations whose graphs are coincident lines has infinitely many solutions and is consistent and dependent.
Try It 5.21
{ 4 x − 5 y = 20 y = 4 5 x − 4 { 4 x − 5 y = 20 y = 4 5 x − 4
Try It 5.22
{ −2 x − 4 y = 8 y = − 1 2 x − 2 { −2 x − 4 y = 8 y = − 1 2 x − 2
Solve Applications of Systems of Equations by Graphing
We will use the same problem solving strategy we used in Math Models to set up and solve applications of systems of linear equations. We’ll modify the strategy slightly here to make it appropriate for systems of equations.
Use a problem solving strategy for systems of linear equations.
- Step 1. Read the problem. Make sure all the words and ideas are understood.
Step 2. Identify what we are looking for.
Step 3. Name what we are looking for. Choose variables to represent those quantities.
Step 4. Translate into a system of equations.
Step 5. Solve the system of equations using good algebra techniques.
Step 6. Check the answer in the problem and make sure it makes sense.
Step 7. Answer the question with a complete sentence.
Step 5 is where we will use the method introduced in this section. We will graph the equations and find the solution.
Example 5.12
Sondra is making 10 quarts of punch from fruit juice and club soda. The number of quarts of fruit juice is 4 times the number of quarts of club soda. How many quarts of fruit juice and how many quarts of club soda does Sondra need?
Step 1. Read the problem.
We are looking for the number of quarts of fruit juice and the number of quarts of club soda that Sondra will need.
Let f = f = number of quarts of fruit juice. c = c = number of quarts of club soda
We now have the system. { f + c = 10 f = 4 c { f + c = 10 f = 4 c
The point of intersection (2, 8) is the solution. This means Sondra needs 2 quarts of club soda and 8 quarts of fruit juice.
Does this make sense in the problem?
Yes, the number of quarts of fruit juice, 8 is 4 times the number of quarts of club soda, 2.
Yes, 10 quarts of punch is 8 quarts of fruit juice plus 2 quarts of club soda.
Sondra needs 8 quarts of fruit juice and 2 quarts of soda.
Try It 5.23
Manny is making 12 quarts of orange juice from concentrate and water. The number of quarts of water is 3 times the number of quarts of concentrate. How many quarts of concentrate and how many quarts of water does Manny need?
Try It 5.24
Alisha is making an 18 ounce coffee beverage that is made from brewed coffee and milk. The number of ounces of brewed coffee is 5 times greater than the number of ounces of milk. How many ounces of coffee and how many ounces of milk does Alisha need?
Access these online resources for additional instruction and practice with solving systems of equations by graphing.
- Instructional Video Solving Linear Systems by Graphing
- Instructional Video Solve by Graphing
Section 5.1 Exercises
Practice makes perfect.
Determine Whether an Ordered Pair is a Solution of a System of Equations . In the following exercises, determine if the following points are solutions to the given system of equations.
{ 2 x − 6 y = 0 3 x − 4 y = 5 { 2 x − 6 y = 0 3 x − 4 y = 5
ⓐ ( 3 , 1 ) ( 3 , 1 ) ⓑ ( −3 , 4 ) ( −3 , 4 )
{ 7 x − 4 y = −1 −3 x − 2 y = 1 { 7 x − 4 y = −1 −3 x − 2 y = 1
ⓐ ( 1 , 2 ) ( 1 , 2 ) ⓑ ( 1 , −2 ) ( 1 , −2 )
{ 2 x + y = 5 x + y = 1 { 2 x + y = 5 x + y = 1
ⓐ ( 4 , −3 ) ( 4 , −3 ) ⓑ ( 2 , 0 ) ( 2 , 0 )
{ −3 x + y = 8 − x + 2 y = −9 { −3 x + y = 8 − x + 2 y = −9
ⓐ ( −5 , −7 ) ( −5 , −7 ) ⓑ ( −5 , 7 ) ( −5 , 7 )
{ x + y = 2 y = 3 4 x { x + y = 2 y = 3 4 x
ⓐ ( 8 7 , 6 7 ) ( 8 7 , 6 7 ) ⓑ ( 1 , 3 4 ) ( 1 , 3 4 )
{ x + y = 1 y = 2 5 x { x + y = 1 y = 2 5 x
ⓐ ( 5 7 , 2 7 ) ( 5 7 , 2 7 ) ⓑ ( 5 , 2 ) ( 5 , 2 )
{ x + 5 y = 10 y = 3 5 x + 1 { x + 5 y = 10 y = 3 5 x + 1
ⓐ ( −10 , 4 ) ( −10 , 4 ) ⓑ ( 5 4 , 7 4 ) ( 5 4 , 7 4 )
{ x + 3 y = 9 y = 2 3 x − 2 { x + 3 y = 9 y = 2 3 x − 2
ⓐ ( −6 , 5 ) ( −6 , 5 ) ⓑ ( 5 , 4 3 ) ( 5 , 4 3 )
Solve a System of Linear Equations by Graphing In the following exercises, solve the following systems of equations by graphing.
{ 3 x + y = −3 2 x + 3 y = 5 { 3 x + y = −3 2 x + 3 y = 5
{ − x + y = 2 2 x + y = −4 { − x + y = 2 2 x + y = −4
{ −3 x + y = −1 2 x + y = 4 { −3 x + y = −1 2 x + y = 4
{ −2 x + 3 y = −3 x + y = 4 { −2 x + 3 y = −3 x + y = 4
{ y = x + 2 y = −2 x + 2 { y = x + 2 y = −2 x + 2
{ y = x − 2 y = −3 x + 2 { y = x − 2 y = −3 x + 2
{ y = 3 2 x + 1 y = − 1 2 x + 5 { y = 3 2 x + 1 y = − 1 2 x + 5
{ y = 2 3 x − 2 y = − 1 3 x − 5 { y = 2 3 x − 2 y = − 1 3 x − 5
{ − x + y = −3 4 x + 4 y = 4 { − x + y = −3 4 x + 4 y = 4
{ x − y = 3 2 x − y = 4 { x − y = 3 2 x − y = 4
{ −3 x + y = −2 4 x − 2 y = 6 { −3 x + y = −2 4 x − 2 y = 6
{ x + y = 5 2 x − y = 4 { x + y = 5 2 x − y = 4
{ x − y = 2 2 x − y = 6 { x − y = 2 2 x − y = 6
{ x + y = 2 x − y = 0 { x + y = 2 x − y = 0
{ x + y = 6 x − y = −8 { x + y = 6 x − y = −8
{ x + y = −5 x − y = 3 { x + y = −5 x − y = 3
{ x + y = 4 x − y = 0 { x + y = 4 x − y = 0
{ x + y = −4 − x + 2 y = −2 { x + y = −4 − x + 2 y = −2
{ − x + 3 y = 3 x + 3 y = 3 { − x + 3 y = 3 x + 3 y = 3
{ −2 x + 3 y = 3 x + 3 y = 12 { −2 x + 3 y = 3 x + 3 y = 12
{ 2 x − y = 4 2 x + 3 y = 12 { 2 x − y = 4 2 x + 3 y = 12
{ 2 x + 3 y = 6 y = −2 { 2 x + 3 y = 6 y = −2
{ −2 x + y = 2 y = 4 { −2 x + y = 2 y = 4
{ x − 3 y = −3 y = 2 { x − 3 y = −3 y = 2
{ 2 x − 2 y = 8 y = −3 { 2 x − 2 y = 8 y = −3
{ 2 x − y = −1 x = 1 { 2 x − y = −1 x = 1
{ x + 2 y = 2 x = −2 { x + 2 y = 2 x = −2
{ x − 3 y = −6 x = −3 { x − 3 y = −6 x = −3
{ x + y = 4 x = 1 { x + y = 4 x = 1
{ 4 x − 3 y = 8 8 x − 6 y = 14 { 4 x − 3 y = 8 8 x − 6 y = 14
{ x + 3 y = 4 −2 x − 6 y = 3 { x + 3 y = 4 −2 x − 6 y = 3
{ −2 x + 4 y = 4 y = 1 2 x { −2 x + 4 y = 4 y = 1 2 x
{ 3 x + 5 y = 10 y = − 3 5 x + 1 { 3 x + 5 y = 10 y = − 3 5 x + 1
{ x = −3 y + 4 2 x + 6 y = 8 { x = −3 y + 4 2 x + 6 y = 8
{ 4 x = 3 y + 7 8 x − 6 y = 14 { 4 x = 3 y + 7 8 x − 6 y = 14
{ 2 x + y = 6 −8 x − 4 y = −24 { 2 x + y = 6 −8 x − 4 y = −24
{ 5 x + 2 y = 7 −10 x − 4 y = −14 { 5 x + 2 y = 7 −10 x − 4 y = −14
{ x + 3 y = −6 4 y = − 4 3 x − 8 { x + 3 y = −6 4 y = − 4 3 x − 8
{ − x + 2 y = −6 y = − 1 2 x − 1 { − x + 2 y = −6 y = − 1 2 x − 1
{ −3 x + 2 y = −2 y = − x + 4 { −3 x + 2 y = −2 y = − x + 4
{ − x + 2 y = −2 y = − x − 1 { − x + 2 y = −2 y = − x − 1
Determine the Number of Solutions of a Linear System Without graphing the following systems of equations, determine the number of solutions and then classify the system of equations.
{ y = 2 3 x + 1 −2 x + 3 y = 5 { y = 2 3 x + 1 −2 x + 3 y = 5
{ y = 1 3 x + 2 x − 3 y = 9 { y = 1 3 x + 2 x − 3 y = 9
{ y = −2 x + 1 4 x + 2 y = 8 { y = −2 x + 1 4 x + 2 y = 8
{ y = 3 x + 4 9 x − 3 y = 18 { y = 3 x + 4 9 x − 3 y = 18
{ y = 2 3 x + 1 2 x − 3 y = 7 { y = 2 3 x + 1 2 x − 3 y = 7
{ 3 x + 4 y = 12 y = −3 x − 1 { 3 x + 4 y = 12 y = −3 x − 1
{ 4 x + 2 y = 10 4 x − 2 y = −6 { 4 x + 2 y = 10 4 x − 2 y = −6
{ 5 x + 3 y = 4 2 x − 3 y = 5 { 5 x + 3 y = 4 2 x − 3 y = 5
{ y = − 1 2 x + 5 x + 2 y = 10 { y = − 1 2 x + 5 x + 2 y = 10
{ y = x + 1 − x + y = 1 { y = x + 1 − x + y = 1
{ y = 2 x + 3 2 x − y = −3 { y = 2 x + 3 2 x − y = −3
{ 5 x − 2 y = 10 y = 5 2 x − 5 { 5 x − 2 y = 10 y = 5 2 x − 5
Solve Applications of Systems of Equations by Graphing In the following exercises, solve.
Molly is making strawberry infused water. For each ounce of strawberry juice, she uses three times as many ounces of water. How many ounces of strawberry juice and how many ounces of water does she need to make 64 ounces of strawberry infused water?
Jamal is making a snack mix that contains only pretzels and nuts. For every ounce of nuts, he will use 2 ounces of pretzels. How many ounces of pretzels and how many ounces of nuts does he need to make 45 ounces of snack mix?
Enrique is making a party mix that contains raisins and nuts. For each ounce of nuts, he uses twice the amount of raisins. How many ounces of nuts and how many ounces of raisins does he need to make 24 ounces of party mix?
Owen is making lemonade from concentrate. The number of quarts of water he needs is 4 times the number of quarts of concentrate. How many quarts of water and how many quarts of concentrate does Owen need to make 100 quarts of lemonade?
Everyday Math
Leo is planning his spring flower garden. He wants to plant tulip and daffodil bulbs. He will plant 6 times as many daffodil bulbs as tulip bulbs. If he wants to plant 350 bulbs, how many tulip bulbs and how many daffodil bulbs should he plant?
A marketing company surveys 1,200 people. They surveyed twice as many females as males. How many males and females did they survey?
Writing Exercises
In a system of linear equations, the two equations have the same slope. Describe the possible solutions to the system.
In a system of linear equations, the two equations have the same intercepts. Describe the possible solutions to the system.
After completing the exercises, use this checklist to evaluate your mastery of the objectives of this section.
If most of your checks were:
…confidently. Congratulations! You have achieved the objectives in this section. Reflect on the study skills you used so that you can continue to use them. What did you do to become confident of your ability to do these things? Be specific.
…with some help. This must be addressed quickly because topics you do not master become potholes in your road to success. In math every topic builds upon previous work. It is important to make sure you have a strong foundation before you move on. Whom can you ask for help? Your fellow classmates and instructor are good resources. Is there a place on campus where math tutors are available? Can your study skills be improved?
…no - I don’t get it! This is a warning sign and you must not ignore it. You should get help right away or you will quickly be overwhelmed. See your instructor as soon as you can to discuss your situation. Together you can come up with a plan to get you the help you need.
This book may not be used in the training of large language models or otherwise be ingested into large language models or generative AI offerings without OpenStax's permission.
Want to cite, share, or modify this book? This book uses the Creative Commons Attribution License and you must attribute OpenStax.
Access for free at https://openstax.org/books/elementary-algebra-2e/pages/1-introduction
- Authors: Lynn Marecek, MaryAnne Anthony-Smith, Andrea Honeycutt Mathis
- Publisher/website: OpenStax
- Book title: Elementary Algebra 2e
- Publication date: Apr 22, 2020
- Location: Houston, Texas
- Book URL: https://openstax.org/books/elementary-algebra-2e/pages/1-introduction
- Section URL: https://openstax.org/books/elementary-algebra-2e/pages/5-1-solve-systems-of-equations-by-graphing
© Jul 24, 2024 OpenStax. Textbook content produced by OpenStax is licensed under a Creative Commons Attribution License . The OpenStax name, OpenStax logo, OpenStax book covers, OpenStax CNX name, and OpenStax CNX logo are not subject to the Creative Commons license and may not be reproduced without the prior and express written consent of Rice University.
Problem Solving with Volume: Water (optional)
Warm-up: Notice and Wonder: Cubic Centimeters and Grams (10 minutes)
CCSS Standards
Routines and Access
Instructional Routines
- Notice and Wonder
The purpose of this warm-up is for students to observe the relationship between the different types of units in the metric system. By contrast, in the standard system, it is not easy to see the relationship between inches, cups, and pounds. While students may notice and wonder many things about this image, conversions between liquid volume units (cups, gallons, liters) and regular volume units (cubic centimeters, cubic inches, cubic feet) are the important discussion points.
- Groups of 2
- Display the image.
- “What do you notice? What do you wonder?”
- 1 minute: quiet think time
- “Discuss your thinking with your partner.”
- 1 minute: partner discussion
- Share and record responses.
Student Facing
What do you notice? What do you wonder?

Attribution: By nclm. CC BY-SA 4.0. Wikimedia Commons. Source .
Student Response
For access, consult one of our IM Certified Partners .
Activity Synthesis
- Highlight that the cube represents 1 cubic centimeter or 1 mL of water and one mL of water weighs 1 g.
- The picture shows the relationships between length, capacity (or volume), and weight in the metric system.
Activity 1: Catching Rainfall (15 minutes)
Access for English Learners
Access for Students with Disabilities
- Representation
The purpose of this activity is for students to estimate how much water falls on the roof of a house, given a particular amount of rainfall. For this calculation, standard units work well as the area of the roof could be given in square feet, for example, and the rain in inches. A conversion would readily give the volume in cubic feet or inches. But, the standard units used to measure volume are cups, pints, quarts, and gallons so more work would need to be done in order to figure out how many gallons, for example, there are in a cubic foot. With the metric system, liquid volume units (liters) and regular volume units (cubic centimeters) are naturally connected.
- “About how big is a square meter?” (It's about the size of my desk top.)
- “About how many square meters do you think there are in the classroom floor?” (maybe 100)
- 5 minutes: independent work time
- 5 minutes: partner work time
Here is a diagram showing the roof of a house.
What is the area of the roof?
Description: 8-sided shape. Straight sides. All side lengths meet at right angles. Side lengths. Bottom, 10 meters. Left side rises 3 meters, then goes left, blank, and goes up 8 meters. Top side length, 15 meters. Right side, blank, then goes left, blank, and down, blank.
- Each month an average of 5 cm of rain falls on the house. How many cubic cm of rain is that?
- There are 1,000 cubic cm in 1 liter. How many liters of water fall on the house?
- You want to build a reservoir to catch the rain that falls so you can use the water. What side lengths would you suggest for the reservoir? Explain or show your reasoning.
- “When did you have to convert units during the activity?” (I needed to convert meters to centimeters since the roof is given in meters and the rain is given in centimeters. I needed to convert cubic centimeters to liters.)
- “How did you make the calculations for the conversions?” (the conversions required multiplying or dividing by powers of 10. I multiplied by 100 to convert m to cm and I divided by 1,000 to convert cubic centimeters to liters.)
- “Do you think that you could make a container to capture all of the rainfall?” (Yes, I think that a 2 meter cube is big but it's not so big that it would not fit near the house. Or we could use several containers that are a little smaller.)
Activity 2: How Much Water? (20 minutes)
The purpose of this activity is for students to find out if the amount of water that falls on the house is sufficient for many of the daily household chores that use water. This will require a lot of estimation and will vary from house to house. How much of the calculations to leave up to the students is an individual teacher choice and this lesson could easily be extended for another day if the students make well reasoned estimates (some values are given in parentheses) for how much water is used for different activities such as:
- taking baths or showers (150 liters or 80 liters)
- washing clothes (100 liters)
- washing dishes (100 liters)
- washing hands (1 liter)
- flushing the toilet (10 liters)
More estimation comes into play for how often each of these activities happens and this will vary greatly depending on the student. When students make a list of the different things they do in the house that use water and then estimate how much water is used they model with mathematics (MP4).
Consider inviting students to check their estimates by looking at one of their monthly water bills. The bill will usually give the number of gallons of water used and there are almost 4 liters in a gallon.
- After students work on the first problem, pause the class and make a list of the main daily uses of water.
- Depending on how much time is available and the modeling demand level desired, consider estimating together or providing estimates for how much water is used for each purpose.
- 10 minutes: partner work time
- What are some of the ways you use water at home?
- Estimate how much water you use at your home in a month.
- How much rain would need to fall on your home each month to supply all of your water needs?
- What challenges might come up if you tried to use the rainwater that falls on the roof of your home? Do you think it makes sense to try to capture the rain that falls on your home?
- “How can you visualize the volume of water that it uses to take a bath?” (I can picture the bathtub filled up partway with water.)
- “How could you measure the volume of water in the bathtub?” (I could measure the length and width of the tub and the height of the water and multiply them.)
- “Are any of the amounts of water used for different things surprising to you? Why?” (I am surprised by how much water it takes to wash the dishes. It’s almost as much as when you take a bath.)
Lesson Synthesis
“How is measuring the volume of water the same as measuring the volume of the Empire State Building?” (If I know the length, width, and height that the water takes up, then I can multiply them to get the volume, just like the building.)
“How is measuring the volume of water different than measuring the volume of a building?” (Water does not have a simple shape like a building. It needs to be put in a container in order to measure.)
“What is important to remember when measuring volume?” (It’s the amount of space something can hold or that something takes up. I can measure it in cubic units or in liters for a liquid.)
Cool-down: Reflection: Volume (5 minutes)
Student section summary.
We investigated several different complex volume questions. For the ancient pyramids of Egypt we gave an estimate of a couple million cubic meters. Since these pyramids are not rectangular prisms, an estimate is the best we could hope for. Then we estimated the volume of the world's largest wagon, using information from a photograph. Lastly, we investigated the amount of rain that falls on a house and the amount of water our families use in a year.
In each case, we could only make estimates because the situations are all complex. In the previous section we used estimation to check the reasonableness of calculations. In this section we saw that making reasoned estimates is a vital part of applying mathematics to many real world situations.
Exploding Dots
8.9 solutions.
Course Home
As promised, here are my solutions to the questions posed.
1. “Six tenths” says exactly what the number is.
2. Indeed both students are correct. Performing some explosions on Subra’s picture gives JinJin’s picture. (And performing some unexplosions on JinJin’s picture gives Subra’s!)
3. a) B b) C
4. We have, in order, \(\dfrac{1}{20}\), \(\dfrac{1}{5}\), \(\dfrac{4}{5}\), and \(\dfrac{1}{250}\).
5. We have, in order, \(\dfrac{4}{10}=0.4\), \(\dfrac{4}{100}=0.04\), \(\dfrac{5}{100}=0.05\), \(\dfrac{5}{1000}=0.005\), and \(\dfrac{8}{10000}=0.0008\).
6. a) B b) D
7. In order, we have \(0.35\), \(0.64\), \(0.602\), \(0.34\), and \(0.75\).
8. a) As a mixed number it is \(2\dfrac{3}{10}\). Or we could write \(2+\dfrac{3}{10}=\dfrac{20}{10}+\dfrac{3}{10}=\dfrac{23}{10}\).
b) \(17+\dfrac{4}{100}=17\dfrac{1}{25}\).
c) \(1003\dfrac{1003}{10000}\).
9. a) Unexploding one dot in the tenths box does “add” ten dots to the hundredths box.
b) Unexploding one dot in the tenths box does now give us 19 dots in the hundredths box. Unexploding these gives 190 dots in the thousandths box.
c) There isn’t much to say here. One can see that one can convert any one picture to any other by explosions and/or unexplosions.
d) Yes! All the pictures are the same, so 0.19 and 0.190 are the same number.
10. a) \(5.3\)
b) \(7+\dfrac{2}{10}\)
c) \(13.5\)
d) \(106+\dfrac{15}{100}=106.15\)
e) \(3+\dfrac{3}{25}=3+\dfrac{12}{100}=3.12\)
f) \(2+\dfrac{1}{4}=2+\dfrac{25}{100}=2.25\)
g) \(3 + \dfrac{11}{40}=3+\dfrac{275}{1000}=3.275\)
11. \(0.05+0.006=0.056\) and \(0.05-0.006-0.0|5|-6=0.044\). Drawing the dots and boxes makes these answers clear.
12. If I draw dots and boxes, then I agree with Agatha.
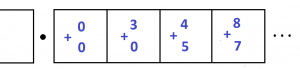
But I don’t agree with Percy.
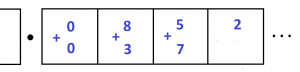
13. Multiplying by \(100\) is the same as multiplying by ten and then multiplying by ten again.
14. We have \(0.04 \times 0.5 = \dfrac{4}{100} \times \dfrac{5}{10}=\dfrac{20}{1000}=\dfrac{2}{100}=0.02\).
(We could have seen this right away too if we noted that \(0.5\) is a half, and one half of \(0.04\) is \(0.02\).)
We have \(1000 \times 0.0385=1000 \times \left(\dfrac{3}{100}+\dfrac{8}{1000}+\dfrac{5}{10000}\right)=30+8+\dfrac{5}{10}=38.5\).
15. We have \(\dfrac{0.9}{10}=\dfrac{9}{100}=0.09\).
We have \(\dfrac{2.34}{1000}=\dfrac{1}{1000}\times \left(2+\dfrac{3}{10}+\dfrac{4}{100}\right)=\dfrac{2}{1000}+\dfrac{3}{10000}+\dfrac{4}{100000}=0.00234\).
We have \(\left(40+\dfrac{4}{100}\right)\times \dfrac{1}{100}=\dfrac{4}{10}+\dfrac{4}{10000}=0.4004\).
16. \(\dfrac{0.75}{25}=\dfrac{75}{2500}=\dfrac{3}{100}=0.03\).
17. This is technically a yes/no question, and the smart answer is no.
For those who answered yes, here are my approaches to the problems.
a) \(0.3 \times \left(5.37-2.07\right)=0.3\times \left(3.3\right) = \dfrac{3}{10}\times \left(3 +\dfrac{3}{10}\right)=\dfrac{9}{10}+\dfrac{9}{100}=0.99\)
b) \(\dfrac{0.1+\left(1.01-0.1\right)}{0.11+0.09}=\dfrac{0.1+\left(0.91\right)}{0.2}=\dfrac{1.01}{0.2}=\dfrac{101}{20}=\dfrac{505}{100}=5.05\)
c) \(\dfrac{\left(0.002+0.2\times 2.-02\right)\left(2.2-0.22\right)}{2.22-0.22}\)
\(=\dfrac{\left(0.002+0.404\right)\left(1.98\right)}{2}\)
\(=\dfrac{\left(0.406\right)\left(1.98\right)}{2}\)
\(=\dfrac{\left(\dfrac{4}{10}+\dfrac{6}{1000}\right)\left(1+\dfrac{9}{10}+\dfrac{8}{100}\right)\times 1000 \times 100}{2\times 1000 \times 100}\)
\(=\dfrac{\left(400+6\right)\left(100+90+8\right)}{2\times 1000 \times 100}\)
\(=\dfrac{406\times 198}{2\times 1000 \times 100}\)
\(=\dfrac{80388}{2\times 100000}\)
\(=\dfrac{40194}{100000}=0.40194\)
18. Do it!
19. Do it too!
20. Do it!
21. You guessed it. Do it!
22. In order, we have \(\dfrac{3}{4}\), \(\dfrac{5}{8}\), \(\dfrac{4}{25}\), \(\dfrac{17}{20}\), and \(\dfrac{5}{80}\).
23. We get \(\dfrac{4}{7}=0.571428 571428 571428 \cdots\).
24. We get \(\dfrac{1}{11}=0.09090909\cdots\).
25. The fractions \(\dfrac{1}{3}\), \(\dfrac{1}{6}\), \(\dfrac{1}{7}\), and \(\dfrac{1}{9}\) have infinitely long decimal expansions.
26 \(\dfrac{133}{6}-22.16666\cdots\).
27. \(\dfrac{255}{11}=23.18181818\cdots\).
28. Do it!
29. Do it too!
30. Yep, do it!
31. Let’s do all our writing in a \(1 \leftarrow 7\) machine. So the number seven is \(10\) and one less than this number is \(6\). Also, notice that multiplying a number by seven in a \(1 \leftarrow 7\) machine has the effect of addending a zero at the end of the number. (Can you see why? It is the same reason why multiplying by ten in a \(1 \leftarrow 10\) machine has the effect of addending a zero.) Multiplying by seven also “shifts the decimal point” one place.
Set \(0.333\cdots = x\).
Multiply each side by seven (which looks like \(10\)). This gives
\(3.3333\cdots = 10x\).
The left side is \(3+0.333\cdots\), that is, \(3\) plus the original number.
\(3+x=10x\)
Subtract \(x\) from both sides.
So \(x\) must equal a half!
32. Can you see how to do it?

Take your understanding to the next level with easy to understand books by James Tanton.
Guides & Solutions
Dive deeper into key topics through detailed, easy to follow guides and solution sets.
Consider supporting G'Day Math! with a donation, of any amount.
Your support is so much appreciated and enables the continued creation of great course content. Thanks!
Ready to Help?
Donations can be made via PayPal and major credit cards. A PayPal account is not required. Many thanks!
An Introduction to Relational Frame Theory (Standard)
8.9 generalized operant example #1 part 2.
Each of the girl’s responses has a different form, but they all have the same effect (receiving praise) in a given context (brother saying “do this” and doing something). Her responses are members of a generalized operant class. Research has shown that imitating another person like this can be trained through operant conditioning. This just means delivering similar effects (consequences) in a given context for a type of response.
| Term | Definition |
|---|---|
| | |
| |
Leave a Comment Cancel reply
You must be logged in to post a comment.
Lesson 8: SEL Problem Solving Lessons For Middle and High Schoolers

- Google Drive™ folder
Also included in

Description
Lesson 8 continues to focus on the Figure Out the Size of the Problem M indfulness strategy. Students are told a story in which one character overreacts to a problem, while a second character matches his reaction to the actual size of the problem. In other words, while the size of the problem remains constant, the two characters have very different reactions. Why people react differently to similar problems is discussed. What a person remembers and realizes are two factors that influence how a person reacts.
This lesson is part of a 16 lesson series. It is recommended that you start with lesson 1: CLICK HERE FOR LESSON 1 or for greater saving check out the LESSON BUNDLES at my store.
MIST is an acronym that helps students tackle problems of all sizes. MIST lessons are comprehensive and explicitly teach students about self-regulation as it relates to how our brains work. Every MIST lesson is easy-to-follow, low prep, provides an overview of content covered, and uses multi-modalities. Lessons are designed for Middle and High School students, can be taught in classrooms or small groups, and are appropriate for students in general and special education.
GOOGLE SLIDE™ Ready
It is recommended that you download the free MIST Problem Solving Visual to complement the lessons. This visual can be used with the MIST lessons and is a useful tool to help scaffold students through problems. Click here to access the free printable download.
Google Slides™ for Lesson 8 : A comprehensive lesson complete with instructions, speaker notes, activities, comprehension questions, and much more.
Each MIST lesson follows a similar format and consists of the following sections:
- Prep and Concepts: Each lesson lists what prep is needed and provides an explanation of the concepts that will be taught in that lesson. The prep is minimal, and everything you need is provided.
- Learning Objectives: Lessons start with statements about what the intended learning objectives are.
- Blast From the Past: This section reflects on past learning. Students are asked to share how they did on the challenge that was assigned the previous lesson.
- Warm-Up Task: This is usually a short writing activity. There are multiple formats students can provide responses. For example, students can write responses on sticky notes and place the notes on a wall, write responses on a paper or index card, or draw pictures of their responses. You may choose to provide each student with a notebook dedicated to Communication Life Hack lessons.
- Check-In: This section asks students to share their responses to the Warm-Up Task. One way to encourage student engagement is for the instructor to share as well.
- The Scoop: This section teaches new content.
- Activity: Each lesson contains an activity for students to apply and practice new concepts.
- Wrap-Up: The Wrap-Up section asks students comprehension questions from the lesson. This section concludes with a carry over challenge activity which students are encouraged to practice on their own.
Here's what the MIST acronym is all about:
M = Mindfulness: M indfulness means being aware of yourself and others.
I = I statement: This is a positive statement that is said to oneself. For example “ I will be OK,” “ I choose to stay calm.”
S = Solution(s): Many of us try to come up with S olutions right away. However, it is difficult to think of logical S olutions when our brains are dysregulated. That is why the M indfulness and I statement steps are so important. When starting as an SLP, my problem solving lessons focused on thinking of Solutions to problems. I did not realize that self-regulation and thoughtful reflection (the T step) are at the core of problem solving.
T = Think: This step encourages reflection. Students can complete this step at any time after the problem occurs and only when they are regulated. It asks students to T hink of the following questions:
- What will I do if this happens again? I tell students that many problems are guaranteed to happen again, and I encourage them to Think through what they will do if and when the problem reoccurs.
- How can I prevent this from happening again? This step challenges students to be proactive by T hinking of strategies to stop the same problems from reoccurring.
- Did my solution work? Sometimes students’ solutions to problems do not have the anticipated results or are maladaptive. When this happens, it is important to reflect.
MIST lessons have been tested and approved by students and teachers. You are the experts, and I would like to thank the special people who participated in lessons and helped improve the MIST series.
A huge thank you to you for considering this product! Your students are on their way to MIST ing their problems!
New Release from Communication Life Hacks:
Active Listening Lessons: Teach your students the foundational strategies to become effective listeners. Each lesson consists of engaging low prep activities that follow a predictable and easy-to-use format. Click here to start the journey.
Picture Credits for Product Preview:
Pixabay.com
K Studio on Freepik.com
RebeccaB Designs
Questions & Answers
Communication life hacks.
- We're hiring
- Help & FAQ
- Privacy policy
- Student privacy
- Terms of service
- Tell us what you think

IMAGES
VIDEO
COMMENTS
This video covers Lesson 8.9 Problems Solving-Find the Whole Group Using Unit Fractions on pages 355-358 of the 3rd grade GO Math textbook.
This lesson shows how to find out how many are in the whole group by knowing a fraction. Here we use unit fractions to show this.
We can use the strategy draw a diagram to solve unit fraction problems. We can draw a diagram to represent all the equal groups in a whole. Then, we can draw...
Problem Solving: Learning Target: Solve multi-step word Fractions problems involving fractions and mixed numbers. Success Criteria: • I can understand a problem. • I can make a plan to solve. • I can solve a problem using an equation. Chapter 8 ⎜ Lesson 9 395 Make Sense of Problems A 7 — 12-foot long piece of one of the male
PRoblem solving Problem Solving • Find the Whole Lesson 8.9 Group Using Unit Fractions Learning Objective You will use the Essential Question How can you use the strategy draw a diagram to solve Strategy draw a diagram to find parts of a fraction problems? group by drawing counters 0 Unlock the Problem World Real Cameron has 4 clown fish in his fish tank.
does each brother get? Draw to model the problem. Step 1 Draw 5 squares for the sandwiches. Step 2 There are 6 brothers. Draw lines to divide each sandwich into 6 equal parts. Step 3 Each brother will get 1 equal part from each sandwich. So, each brother gets 5 sixths of a sandwich. Draw lines to show how much each person gets. Write the answer.
QuickMath will automatically answer the most common problems in algebra, equations and calculus faced by high-school and college students. The algebra section allows you to expand, factor or simplify virtually any expression you choose. It also has commands for splitting fractions into partial fractions, combining several fractions into one and ...
2.2 Use a Problem Solving Strategy; 2.3 Solve a Formula for a Specific Variable; 2.4 Solve Mixture and Uniform Motion Applications; 2.5 Solve Linear Inequalities; 2.6 Solve Compound Inequalities; 2.7 Solve Absolute Value Inequalities
8.9 Variation and Problem Solving. The force F needed to break a board varies inversely with the length l of the board. If it takes 24 pounds of pressure to break a board 2 feet long, how many pounds of pressure will it take to break a board that is 5 feet long? Give your answer as a decimal and do not include units. Follow • 1.
8; 9; Unit 8 Lesson 9. ↓ Skip to main content. Activity 9.1; Activity 9.2; Activity 9.3; Lesson 9 Summary; Practice Problems; Lesson 9 The Converse. Let's figure out if a triangle is a right triangle. Learning Targets: I can explain why it is true that if the side lengths of a triangle satisfy the equation
Chapter 11 Review for Test on Perimeter and Area. Count Equal Groups - Lesson 3.1. Relate Addition and Multiplication - Lesson 3.2. Skip Count on a Number Line - Lesson 3.3. Problem Solving - Model Multiplication - Lesson 3.4. Model with Arrays - Lesson 3.5. Commutative Property of Multiplication - Lesson 3.6. Multiply with 1 and 0 - Lesson 3.7.
Introduction; 2.1 Solve Equations Using the Subtraction and Addition Properties of Equality; 2.2 Solve Equations using the Division and Multiplication Properties of Equality; 2.3 Solve Equations with Variables and Constants on Both Sides; 2.4 Use a General Strategy to Solve Linear Equations; 2.5 Solve Equations with Fractions or Decimals; 2.6 Solve a Formula for a Specific Variable
Lesson 9. Problem Solving with Volume: Water (optional) Preparation Lesson. ... How much of the calculations to leave up to the students is an individual teacher choice and this lesson could easily be extended for another day if the students make well reasoned estimates (some values are given in parentheses) for how much water is used for ...
8th Grade Math SOL Resources. Online Practice tests from Jefferson Lab. 8.1: The student will. a) simplify numerical expressions involving positive exponents, using rational numbers, order of operations, and properties of operations with real numbers. Definitions, explanations, practice order of operations and exponent problems at math.com.
Exercise 28. Exercise 29. Exercise 30. Exercise 31. Exercise 32. Exercise 33. Exercise 34. Exercise 35. Find step-by-step solutions and answers to Glencoe Math Accelerated - 9780076637980, as well as thousands of textbooks so you can move forward with confidence.
8.9 Solutions. As promised, here are my solutions to the questions posed. 1. "Six tenths" says exactly what the number is. 2. Indeed both students are correct. Performing some explosions on Subra's picture gives JinJin's picture. (And performing some unexplosions on JinJin's picture gives Subra's!)
Explain. Chapter 8. one hundred eighty-five. Larry is telling his sister about using a ruler to measure length. Fill in the blanks with 'inch' or 'foot' to make the sentence true. __ is longer than 1 __ . NBT.5, 2.NBT.7, 2.MD.7, 2.MD.8) Matt put this money in his pocket.
Problem-Solving Steps in Equilibrium Problems (page 274) 1. Identify an object or system in equilibrium. Draw a diagram showing all the forces ... Lesson 11: Equilibrium, Newton's second law, Rolling, Angular Momentum (Sections 8.3-8.9) Lesson 11, page 10 We have completed our study of rotational motion. Try to see how it is analogous to (the ...
Lesson: Problem solving with time Instruct: https://mathexplanation.com/lessons/problem-solving-with-time-1160.html Practice: https://mathexplanation.com...
Lesson 12: Transformation of Stimulus Functions 45 Topics 12.1 Concept Map. 12.2 Definition of Transformation of Stimulus Functions. ... 15.32 Problem Solving Example Part 11. 15.33 Problem Solving Example Part 12. 15.34 Rules and Contingency-Shaped Behavior.
ALL 16 problem solving/self-regulation lessons are included in this bundle!WELCOME TO MIST! MIST is an acronym that helps students tackle problems of all sizes. This bundle consists of the first 8 out of a total of 16 MIST lessons. MIST lessons teach each letter in the acronym along with the foundat