what is the hypothesis of normal distribution

Learning Materials

Business Studies
Combined Science
Computer Science
Engineering
English Literature
Environmental Science
Human Geography
Macroeconomics
Microeconomics
Normal Distribution Hypothesis Test

Hypothesis tests for the normal distribution can be conducted in a very similar way to binomial distribution , e xcept this time we switch our test statistic. These tests are useful as again they help us test claims of normally distributed items.

Millions of flashcards designed to help you ace your studies

Achieve better grades quicker with Premium

Geld-zurück-Garantie, wenn du durch die Prüfung fällst

Review generated flashcards

to start learning or create your own AI flashcards

Start learning or create your own AI flashcards

StudySmarter Editorial Team

Team Normal Distribution Hypothesis Test Teachers

6 minutes reading time
Checked by StudySmarter Editorial Team
Applied Mathematics
Decision Maths
Discrete Mathematics
Logic and Functions
Mechanics Maths
Probability and Statistics
Bayesian Statistics
Bias in Experiments
Binomial Distribution
Binomial Hypothesis Test
Biostatistics
Bivariate Data
Categorical Data Analysis
Categorical Variables
Causal Inference
Central Limit Theorem
Chi Square Test for Goodness of Fit
Chi Square Test for Homogeneity
Chi Square Test for Independence
Chi-Square Distribution
Cluster Analysis
Combining Random Variables
Comparing Data
Comparing Two Means Hypothesis Testing
Conditional Probability
Conducting A Study
Conducting a Survey
Conducting an Experiment
Confidence Interval for Population Mean
Confidence Interval for Population Proportion
Confidence Interval for Slope of Regression Line
Confidence Interval for the Difference of Two Means
Confidence Intervals
Correlation Math
Cox Regression
Cumulative Distribution Function
Cumulative Frequency
Data Analysis
Data Interpretation
Decision Theory
Degrees of Freedom
Discrete Random Variable
Discriminant Analysis
Distributions
Empirical Bayes Methods
Empirical Rule
Errors In Hypothesis Testing
Estimation Theory
Estimator Bias
Events (Probability)
Experimental Design
Factor Analysis
Frequency Polygons
Generalization and Conclusions
Geometric Distribution
Geostatistics
Hierarchical Modeling
Hypothesis Test for Correlation
Hypothesis Test for Regression Slope
Hypothesis Test of Two Population Proportions
Hypothesis Testing
Inference For Distributions Of Categorical Data
Inferences in Statistics
Item Response Theory
Kaplan-Meier Estimate
Kernel Density Estimation
Large Data Set
Lasso Regression
Latent Variable Models
Least Squares Linear Regression
Linear Interpolation
Linear Regression
Logistic Regression
Machine Learning
Mann-Whitney Test
Markov Chains
Mean and Variance of Poisson Distributions
Measures of Central Tendency
Methods of Data Collection
Mixed Models
Multilevel Modeling
Multivariate Analysis
Neyman-Pearson Lemma
Non-parametric Methods
Normal Distribution
Normal Distribution Percentile
Ordinal Regression
Paired T-Test
Parametric Methods
Path Analysis
Point Estimation
Poisson Regression
Principle Components Analysis
Probability
Probability Calculations
Probability Density Function
Probability Distribution
Probability Generating Function
Product Moment Correlation Coefficient
Quantile Regression
Quantitative Variables
Random Effects Model
Random Variables
Randomized Block Design
Regression Analysis
Residual Sum of Squares
Robust Statistics
Sample Mean
Sample Proportion
Sampling Distribution
Sampling Theory
Scatter Graphs
Sequential Analysis
Single Variable Data
Spearman's Rank Correlation
Spearman's Rank Correlation Coefficient
Standard Deviation
Standard Error
Standard Normal Distribution
Statistical Graphs
Statistical Inference
Statistical Measures
Stem and Leaf Graph
Stochastic Processes
Structural Equation Modeling
Sum of Independent Random Variables
Survey Bias
Survival Analysis
Survivor Function
T-distribution
The Power Function
Time Series Analysis
Transforming Random Variables
Tree Diagram
Two Categorical Variables
Two Quantitative Variables
Type I Error
Type II Error
Types of Data in Statistics
Variance for Binomial Distribution
Venn Diagrams
Wilcoxon Test
Zero-Inflated Models
Theoretical and Mathematical Physics

Jump to a key chapter

How do we carry out a hypothesis test for normal distribution?

When we hypothesis test for the mean of a normal distribution we think about looking at the mean of a sample from a population.

So for a random sample of size n of a population, taken from the random variable \(X \sim N(\mu, \sigma^2)\) , the sample mean \(\bar{X}\) can be normally distributed by \(\bar{X} \sim N(\mu, \frac{\sigma^2}{n})\) .

Let's look at an example.

The weight of crisps is each packet is normally distributed with a standard deviation of 2.5g.

The crisp company claims that the crisp packets have a mean weight of 28g. There were numerous complaints that each crisp packet weighs less than this. Therefore a trading inspector investigated this and found in a sample of 50 crisp packets, the mean weight was 27.2g.

Using a 5% significance level and stating the hypothesis, clearly test whether or not the evidence upholds the complaints.

This is an example of a one tailed test. Let's look at an example of a two tailed test.

A machine produces circular discs with a radius R, where R is normally distributed with a mean of 2cm and a standard deviation of 0.3cm.

The machine is serviced and after the service, a random sample of 40 discs is taken to see if the mean has changed from 2cm. The radius is still normally distributed with a standard deviation of 0.3 cm.

The mean is found to be 1.9cm.

Has the mean changed? Test this to a 5% significance level.

Step 5 may be confusing – do we carry out the calculation with \(P(\bar{X} \leq \bar{x})\) or \(P(\bar{X} \geq \bar{x})\)? As a general rule of thumb if the value is between 0 and the mean, then we use \(P(\bar{X} \leq \bar{x})\) . If it is greater than the mean then we use \(P(\bar{X} \geq \bar{x})\) .

How about finding critical values and critical regions?

This is the same idea as in binomial distribution . However, in normal distribution, a calculator can make our lives easier.

The distributions menu has an option called inverse normal.

Here, we enter the significance level (Area), the mean (\(\mu\) ) and the standard deviation (\(\sigma\) ).

The calculator will give us an answer. Let's have a look at an example below.

Wheels are made to measure for a bike. The diameter of the wheel is normally distributed with a mean of 40cm and a standard deviation of 5cm. Some people think that their wheels are too small. Find the critical value of this to a 5% significance level.

In our calculator, in the inverse normal function, we need to enter:

If we perform the inverse normal function we get 31.775732 .

So that is our critical value and our critical region is \(X \leq 31.775732\) .

Let's look at an example with two tails.

Normal distribution hypothesis test two tailed test studysmarter

Hypothesis Test for Normal Distribution - Key takeaways

When we hypothesis test for a normal distribution we are trying to see if the mean is different from the mean stated in the null hypothesis.
We use the sample mean which is \(\bar{X} \sim N(\mu, \frac{\sigma^2}{n})\) .
In two-tailed tests we divide the significance level by two and test on both tails.
When finding critical values we use the calculator inverse normal function entering the area as the significance level.
For two-tailed tests we need to find two critical values on either end of the distribution.

Learn faster with the 0 flashcards about Normal Distribution Hypothesis Test

Already have an account? Log in

Frequently Asked Questions about Normal Distribution Hypothesis Test

How do you test a hypothesis for a normal distribution?

Is hypothesis testing only for a normal distribution?

No, pretty much any distribution can be used when testing a hypothesis. The two distributions that you learn at A-Level are Normal and Binomial.

What statistical hypothesis can be tested in the means of a normal distribution?

We test whether or not the data can support the value of a mean being too low or too high.

Discover learning materials with the free StudySmarter app

About StudySmarter

StudySmarter is a globally recognized educational technology company, offering a holistic learning platform designed for students of all ages and educational levels. Our platform provides learning support for a wide range of subjects, including STEM, Social Sciences, and Languages and also helps students to successfully master various tests and exams worldwide, such as GCSE, A Level, SAT, ACT, Abitur, and more. We offer an extensive library of learning materials, including interactive flashcards, comprehensive textbook solutions, and detailed explanations. The cutting-edge technology and tools we provide help students create their own learning materials. StudySmarter’s content is not only expert-verified but also regularly updated to ensure accuracy and relevance.

Team Math Teachers

Study anywhere. Anytime.Across all devices.

Create a free account to save this explanation..

Save explanations to your personalised space and access them anytime, anywhere!

By signing up, you agree to the Terms and Conditions and the Privacy Policy of StudySmarter.

Join over 22 million students in learning with our StudySmarter App

The first learning app that truly has everything you need to ace your exams in one place

Flashcards & Quizzes
AI Study Assistant
Study Planner
Smart Note-Taking

Join over 22 million students in learning with our StudySmarter App

The Open University
Accessibility hub
Guest user / Sign out
Study with The Open University

My OpenLearn Profile

Personalise your OpenLearn profile, save your favourite content and get recognition for your learning

About this free course

Become an ou student, download this course, share this free course.

Start this free course now. Just create an account and sign in. Enrol and complete the course for a free statement of participation or digital badge if available.

4.1 The normal distribution

Here, you will look at the concept of normal distribution and the bell-shaped curve. The peak point (the top of the bell) represents the most probable occurrences, while other possible occurrences are distributed symmetrically around the peak point, creating a downward-sloping curve on either side of the peak point.

The cartoon shows a bell-shaped curve. The x-axis is titled ‘How high the hill is’ and the y-axis is titled ‘Number of hills’. The top of the bell-shaped curve is labelled ‘Average hill’, but on the lower right tail of the bell-shaped curve is labelled ‘Big hill’.

In order to test hypotheses, you need to calculate the test statistic and compare it with the value in the bell curve. This will be done by using the concept of ‘normal distribution’.

A normal distribution is a probability distribution that is symmetric about the mean, indicating that data near the mean are more likely to occur than data far from it. In graph form, a normal distribution appears as a bell curve. The values in the x-axis of the normal distribution graph represent the z-scores. The test statistic that you wish to use to test the set of hypotheses is the z-score . A z-score is used to measure how far the observation (sample mean) is from the 0 value of the bell curve (population mean). In statistics, this distance is measured by standard deviation. Therefore, when the z-score is equal to 2, the observation is 2 standard deviations away from the value 0 in the normal distribution curve.

A symmetrical graph reminiscent of a bell showing normal distribution.

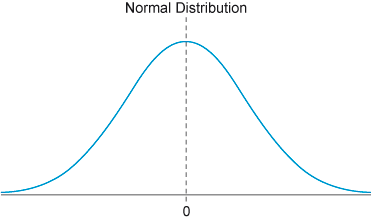
A symmetrical graph reminiscent of a bell. The top of the bell-shaped curve appears where the x-axis is at 0. This is labelled as Normal distribution.